Úvod
Požadavky na zpracování dat kladou výzvy při definici a vytváření matematicko-statistických postupů, které umožňují nacházet nové přístupy. Používají se nové výpočetní postupy, které umožňují provádět analýzy, které ještě nedávno nebyly možné kvůli své složitosti a náročnosti. Jednotlivé statistické sw v sobě již standardně nabízí oblast obecně zvanou data mining, což v překladu přímo znamená dolování dat. V našem příspěvku se zaměříme na možnosti tzv. klasifikačních stromů, které budeme demonstrovat na dotazníkovém šetření a to v sw Statistica 12 firmy Statsoft.
Klasifikace
Metody klasifikační analýzy lze zařadit do vícerozměrných statistických metod. Jejich smyslem je nalézt v datech strukturu založenou na vzájemných vztazích a tuto strukturu pak reprezentovat výzkumníkovi pokud možno srozumitelnou formou (např. grafickou). Obecně má klasifikace za cíl shlukovat pozorované entity do skupin. V jednotlivých skupinách jsou pak takové entity, které jsou si podobné, blízké. Naopak entity, které jsou rozdílné a od sebe odlišné, se vyskytují v různých skupinách.
Klasifikační metody lze rozdělit podle několika způsobů (Pechotová, 2009):
podle typu učení
učení s učitelem
Diskriminační analýza – Discrimination analysis (DA)
Klasifikační stromy – Classification trees
Zobecněny lineární model (logistická regrese) - Generalized Linear Model (GLM)
Neuronové sítě – Neural networks (NN)
učení bez učitele
Shluková analýza - Cluster analysis (hierarchická i nehierarchická)
Analýza hlavních komponent - Principal component analysis(PCA)
Vícerozměrné škálování – Multidimensional scaling(MDS)
podle rozdělení náhodného vektoru
parametrické metody. Zde je nutné splnit předpoklady originálních dat, např. normalita
Diskriminační analýza
Logistická regrese
neparametrické metody – žádné předpoklady data v podstatě splňovat nemusí
Klasifikační stromy a lesy – Classification trees and forests
Neuronové sítě – Neural networks
podle rozdělení náhodného vektoru
regresní
klasifikační
V textu se zaměříme na metodu tvorby klasifikačních stromů. Ostatní metody jsou popsány ve velké množině zdrojů, které namátkou uvádíme v přehledu použitých zdrojů na konci textu
Diskriminační analýza
Meloun & Militký (2004), Anděl (2007), Forbelská (2000), McLachlan (2004)
Klasifikační stromy
Breiman (1998), Ripley (2000), Komprdová (2012)
Neuronové sítě
Bishop (2000), Fausett (1994), Jiřina (2008), Rojas (1996)
Zobecněny lineární model, Logistická regrese, Shluková analýza, Analýza hlavních komponent, Vícerozměrné škálování
Hosmer, Lemeshow, & Sturdivant (2013); Zvára (2008); Meloun & Militký (2004); Řezanková, Marek, & Vrabec (2001); STATSOFT (2010); Hebák, Hustopecký, Jarošová, & Pecáková (2007); Hebák, Hustopecký, & Malá (2006); Hebák et al (2007); Hendl (2004)
Klasifikační stromy
Klasifikační stromy patří mezi neparametrické metody. Vzorky se klasifikují lineárně a hierarchicky do konečného (malého) předem daného počtu tříd. Jedná se o posloupnost rozhodnutí, jejímž výsledkem je zařazení objektu do jedné ze skupin na základě vlastnosti zkoumaného objektu. V každém uzlu je určena proměnná, podle které dělíme datový soubor a hranice, která určuje, kde se dělení má provést. Kořen obsahuje celý datový soubor. Z každého uzlu vyrůstají dvě (binární strom) nebo více větví. Každý list představuje některou ze skupin.
Klasifikační stromy se nejčastěji využívají k nalezení vzájemných vztahů a struktuře v datech. Z toho pohledu se jedná o explorativní metodu.
Tvorba klasifikačního stromu je podmíněna mnoha kroky a pravidly. V algoritmech popisujících vytváření stromu existuje mnoho způsobů, jak vybírat proměnné, na základě nichž jsou data dělena. Obecný princip je však stejný: vybrat takovou proměnnou, která rozdělí data na pokud možno nejhomogennější podksupiny. Druhým podstatným principem je okamžik zastavení růstu stromu. Nabízí se způsoby, kdy:
další dělení není statisticky významné
velikost chyby v poduzlech (růst se zastaví v okamžiku, kdy procentuální úspěšnost nesprávné klasifikace překročí zadanou hodnotu)
počet vzorků v koncovém uzlu
počet terminálních uzlů
Zde proti sobě stojí dvě protichůdné požadavky na strom. Musí být přesný (specializovaný), ale zároveň i obecný, aby byl schopen postihnout další obecné závislosti vyskytující se v datech. Při tvorbě stromu lze s výhodou použít způsob křížová-validace, kdy jsou původní data rozdělena do k skupin. Každá skupina je použita jako testovací a zbytek pak pro tvorbu stromu. Tento algoritmus se opakuje k krát. Z výsledných k stromů zjistíme predikční schopnosti stromu.
Mezi výhody klasifikačních stromů patří:
intuitivní grafická intepretace.
na data obecně neklademe žádné požadavky. Nemusí být zajištěna normalita dat, data mohou být vysoce korelované
prediktory mohou být spojité, ordinální i kategoriální proměnné
Hlavní nevýhodou klasifikačních stromů je jasně
tvar stromu záleží na vstupních dat
nejsou vhodné pro malý počet měření, kdy ani pomocné techniky (křížová-validace) nepomohou
Z jednotlivých algoritmů učení popíšeme dva základní
CART (Classification and Regression Trees). Je generován binární strom (každý uzel má právě 2 poduzly). Výběr nejlepšího atributu pro výběr je prováděn na základě entropie a Gini indexu. Metoda umí seřadit jednotlivé proměnné podle jejich významu (importance) při klasifikaci
CHAID (Chi-squared Automatic Interaction Detector). Tato metoda používá pro tvorbu stromu kritérium chí-kvadrát ↓2. Algoritmus postupně seskupuje všechny hodnoty sledované proměnné až do podksupin velikosti 2. Poté se vybere hodnota taková, která je pro další větvení nejvhodnější. Obecně tak CHAID tvoří stromy s větším počtem uzlů (uzel má více poduzlů), Ve skupinách o velikosti 2 se na základě ↓2 zvolí dvojice, které jsou si nejpodobnější. Strom se již dále nevětví, pokud další větvení již nepřispěje ke zlepšení klasifikace.
Příklad: Dotazníkové šetření
Aplikaci vybraných klasifikačních metod budeme demonstrovat na dotazníkovém šetření realizovaném na Fakultě sportovních studií Masarykovy univerzity.
Zkoumaný soubor tvoří 5878 probandů, zástupců běžné populace v České republice, z toho 3032 žen a 2846 mužů. Dotazníkové šetření bylo realizováno v rámci projektu CZ.1.07/2.3.00/20.0044 „Vytvoření výzkumného týmu vedeného reintegrovaným českým vědcem za účelem zjišťování úrovně pohybové aktivity (inaktivity) u vybraných věkových skupin mužů a žen v ČR“.
K zjišťování pohybové aktivity běžné populace v ČR jsme použili upravený standardizovaný dotazník „International Physical Activity Questionnaire“ (Craig et al., 2003) v české verzi. Pohybová aktivita dospělých byla posuzována podle času věnovanému intenzivní PA, středně zatěžující PA a chůzi. Respondenti hodnotili též charakter své práce, způsob dopravy do zaměstnání, frekvenci doby strávené chůzí a jízdou na kole, informaci o jejich aktivním sportování v rámci jakékoliv sportovní organizace. Dále popisovali bolestivost zad a kloubů, zda kouří a konzumují alkoholické nápoje. Na závěr poskytli základní demografické údaje jako místo trvalého bydliště, velikost sídla, rodinný stav, dosažené vzdělání a věk.
V rámci tohoto šetření jsme si položili otázku, zda lze nalézt v datech množinu prediktorů (nezávislé proměnné), pomocí nichž jsme schopni klasifikovat data a pozorovat jejich vliv na závislou proměnnou, což je bolestivost zad. Jinými slovy, nalézt v datech takovou datovou strukturu, která napoví, co nejvíce ovlivňuje bolestivost zad. Výsledky jsou samozřejmě závislé na odpovědích respondentů.
Sledované proměnné jsou:
Závislá:
bolest zad (Nikdy, Občas, Často)
Nezávislé:
věková skupina (18-29, 30-39, 40-49, 50-59, 60-69, >70)
pohlaví (muž, žena)
typ zaměstnání (fyzická práce, sedavé zaměstnání, fyzické i sedavé zaměstnání, nepracuji)
doprava do zaměstnání (pěšky, na kole, „autobus, vlak, MHD“, auto, do zaměstnání se nedopravuji)
intenzivní pohybová aktivita (neprovádím, do 1 hodiny, 1 – 3 hodiny, 3 – 6 hodin, více než 6 hodin)
středně zatěžující pohybová aktivita (neprovádím, do 1 hodiny, 1 – 3 hodiny, 3 – 6 hodin, více než 6 hodin)
chůze denně (žádná, cca 30 minut, cca 60 minut, cca 120 minut)
kolo (ne, téměř každý den, občas -např. 1x za měsíc, výjimečně - např. 1x za půl roku)
sportovní aktivita (ano, ne)
bolest kloubů (nikdy, občas, často)
kouření (ano, ne)
alkohol (ne, občas, pravidelně)
velikost sídla (obec ≤ 999 obyvatel, menší město 1000 – 29 999 obyvatel, středně velké město 30 000 – 99 999 obyvatel, velké město ≥100 000 obyvatel)
rodinný stav (svobodný, ženatý/vdaná, rozvedený/rozvedená, ovdovělý/ovdovělá)
vzdělání (základní, SŠ – vyučen, SŠ – maturita, vysokoškolské)
Metoda CART
Výsledkem je strom na obr. 1
Obr. 1 Klasifikační strom (CART)
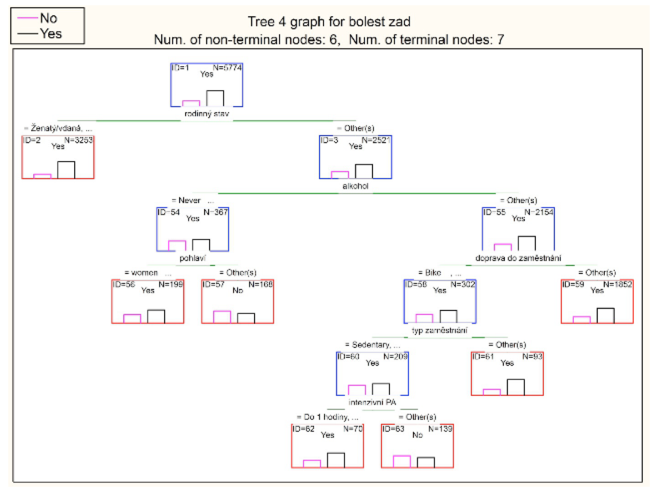
Z výsledného stromu můžeme vyčíst následující skutečnosti a závislosti:
každý uzel má svůj identifikátor (ID) s uvedeným počtem respondentů patřících do tohoto uzlu, ve spodní části uzlu je pak graficky znázorněn poměr odpovědí u sledované závislé proměnné. V uzlu ID=1 se jedná o grafické znázornění počtu respondentů, které nebolí záda (levý obdélník) a bolí záda (pravý obdélník). Logickou konstrukcí je odpověď na otázku: Bolest zad s odpovědí YES? levý obdélník (NO), pravý obdélník (YES).
primárním prediktorem je rodinný stav. Levý podstrom je tvořen kategoriemi (ženatý/vdaná, rozvedený/rozvedená), pravý podstrom pak kategorií (svobodní)
U svobodných je pak nejvyšším prediktorem konzumace alkoholu. Levý podstrom jsou respondenti uvádějící „never“, nikdy alkohol nepili či nepijí. Dále jsou pak děleni jen podle pohlaví (muži, ženy)
U svobodných, kteří uvedli konzumaci alkoholu je dalším limitujícím prediktorem způsob dopravy do zaměstnání. Levý podstrom jsou cyklisté, pravý podstrom jsou ostatní způsoby dopravy do zaměstnání
Cyklisté jsou pak děleny podle typu zaměstnání na sedavé a „nepracuji“ a ti jsou rozděleni podle množství intenzivní pohybové aktivity (do 1 hodiny“ a „více ne 6 hod“) a ostatní (tedy od 1 – 6 hodin intenzivní pohybové aktivity)
Pokud bychom měli iteračně vysledovat, ve kterém poduzlu jsou respondenti, které záda převážně nebolí, pak to je uzel ID 63. Svobodní, konzumující alkohol, cyklisté se sedavým zaměstnáním s množstvím intenzivní pohybové aktivity od 1 do 6 hodin týdně.
Podle důležitosti (importance) jsou pak proměnné seřazeny na obr. 2. Je to seznam takových proměnných, které byly zohledněny během výpočtu konečného stromu, ačkoliv nakonec nebyly zařazeny mezi proměnné, sloužící k rozdělování stromu. Zde nacházíme ty pravé determinanty pro závislou proměnnou „bolest zad“. Jedná se o intenzivní pohybovou aktivitu, sportovní aktivitu, pohlaví, množství chůze denně a typ zaměstnání.
Je nutné podotknout, že seznam „importance“ proměnných závisí na konkrétním vytvořeném stromě.
Obr. 2 Klasifikační strom CART – důležitost
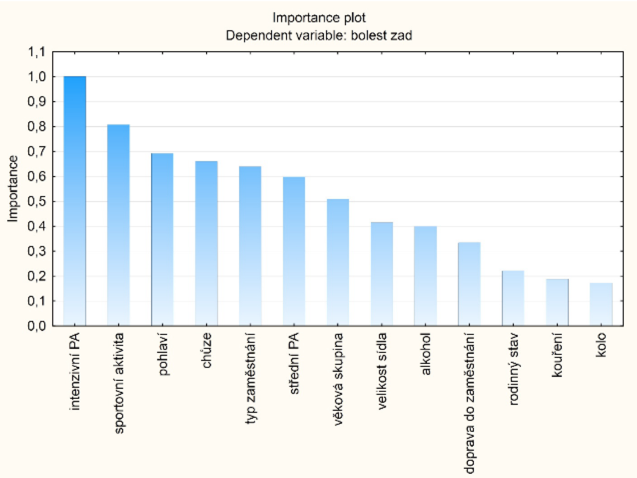
Metoda CHAID
Výsledkem je strom na obr. 3
Obr. 3 Klasifikační strom CHAID
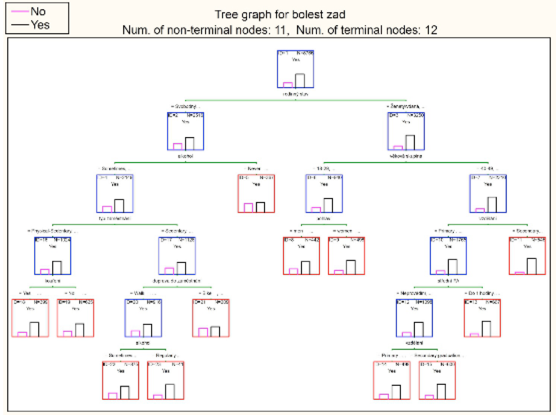
Z obr. 3 můžeme sledovat podobné výsledky metodě CART. Interpretace výsledného klasifikačního stromu jsou shodná, jako u metody CART. Zajímavější je uzel ID=21. Zde jsou zahrnuti respondenti se stejným poměrem bolestivosti a „nebolení“ zad. Jsou to svobodní, občas konzumující alkohol, se sedavým zaměstnáním a dopravující se do zaměstnání na kole?
Shrnutí
U obou klasifikačních metod (CART a CHAID) vidíme podobné prediktory stavu, kdy respondenti uvádějí, že je záda nebolí. Vytvořené klasifikační stromy nabízejí širokou paletu interpretace, zároveň lze stromy modifikovat přidáním nebo odebráním nezávislé proměnné, čímž lze vytvořit zcela jiný strom, který bude opět popisovat datovou strukturu skrytou v datech. Nicméně po zkušenostech s tvorbou jednotlivých klasifikačních stromů a nastavováním jednotlivých parametrů, můžeme konstatovat, že pokud v datech existuje skrytá struktura a závislost mezi kategoriemi, pak ji rozpozná většina statistických postupů a metod.
Úloha klasifikace neboli zařazení objektů do podobných tříd je velmi rozšířená a zcela běžná ve všech typech výzkumů. S nástupem výpočetní síly matematických a statistických software roste i oblíbenosti jednotlivých klasifikačních metod. Jak ovšem platí o téměř každém matematickém nebo statistickém postupu, je nutné znát nejen silné, ale i slabé stránky či omezení jednotlivých postupů. Nejinak je tomu u klasifikačních stromů. Ke všem výsledkům a výstupům musí odpovědně přistoupit výzkumník či řešitelský tým a zabývat se správnou věcnou interpretací. Jedině tehdy lze s výhodou využívat sofistikované výpočetní postupy.