Výběr optimálního tréninku u nesportovců na základě metabolické odezvy

Stále důkladnějšími znalostmi metabolických systémů chceme přispět k jejich využití ve sportovní praxi, při plánování pohybových zatížení. Stejně tak jako mnozí ostatní chceme lépe charakterizovat účinky cvičení na metabolickou odezvu, především na energetický výdej sportujícího organismu.

O rozdílném efektu sportovních tréninků v různých intenzitách zátěže víme mnohé. Téma studie je stavěno na myšlence, zdali je možné zjistit, jaké pohybové zatížení je vhodné doporučit běžnému člověku, který se pohybuje občasně, nemá rozvinuty aerobní schopnosti jako pravidelně sportující atlet a chce začít se sportem pro zlepšení svého fyzického a konstitučního stavu. Chceme zjistit, zdali se námi měřené metabolické parametry budou lišit ve svých hodnotách při pohybových aktivitách různého charakteru, při aerobní pohybové aktivitě a anaerobním, do jisté míry silově vytrvalostním zatížením.

Doposud byla provedena pilotní studie za účelem ověření proveditelnosti výzkumu (jaro 2012).

Metodika

Vybrali jsme 2 typy testovacích tréninků:

1. aerobní trénink = 60 minut soustavné chůze a/nebo běhu rychlostí 7–10 km/hod v nulovém sklonu na běhacím trenažéru

2. silově vytrvalostní posilovací trénink = 60 minut posilovacího tréninku, jsou v něm zahrnuty všechny složky pohybové lekce, tedy úvodní, protahovací, hlavní a zakončovací část; hlavní část tvoří 35 - 38 minut

Ve studii jsme si vymezili následující pojmy:

Nesportovec

Názvem nesportovec (nesportovci) jsme označovali konkrétní testovací osobu (osoby) pro naši studii.

Pojem není vědecky definován. Naše označení cílí na fakt, že jsme osoby pro testování nevybírali z řad profesionálních sportovců (je spojeno s přívlastkem vrcholový nebo výkonostní), ale podle kritéria úrovně provozování sportu, přičemž jsme vybírali osoby z oblasti rekreačních sportovců - pod heslem příležitostně sportující. Výběr probandů jsme učinili pomocí námi sestaveného dotazníku.

Optimální trénink

Optimálním tréninkem rozumíme nejlépe vyhovující přípravu a zlepšování se za účelem dosažení stanoveného cíle.

Měření probíhá ventilátorem Oxycon Mobile, tedy přenosným analyzátorem dechových plynů, pomocí kterého je možné změřit a zaznamenat dechovou analýzu pohybující se osoby. 30 námi vybraných probandů bylo rozděleno náhodným tříděním do 2 skupin po 15 osobách.

Během testovacího 3měsíčního období jsme se skupinami provedli 24 tréninkových jednotek, přičemž jsme v první a poslední tréninkové jednotce provedli testování - měření vybraných parametrů.

Postup měření:

Během testovacího 3měsíčního období jsme s oběmi náhodně vybranými skupinami provedli 24 tréninkových jednotek, přičemž jsme v první a poslední tréninkové jednotce provedli testování - měření námi vybraných parametrů. Po dokončení testovacího období jsme nashromážděná data statisticky zpracovali pomocí programu Matlab.

Výběr měřených fyziologických parametrů pro statistické zpracování

Pomocí přístroje Oxycon mobile jsme provedli měření fyziologických parametrů nabývajících hodnot při zatížení.  Z naměřených hodnot přístrojem Oxycon Mobile jsme vybrali následující parametry:

 

MET – (The Metabolic Equivalent of Task) - metabolický ekvivalent

vyjadřuje skutečnost, kolikrát je jedinec schopen v průběhu zátěže zvýšit svoji klidovou spotřebu kyslíku. Během zátěže hodnota příjmu kyslíku mnohonásobně stoupá.

Za bazálních podmínek v klidu a bdělém stavu odpovídá u dospělých přibližně 3,5 ml.kg^-1.min^-1, u dětí až 4 ml.kg^-1.min^-1

Vyjadřuje maximální funkční aerobní kapacitu jedince a její určování se používá při testování funkční zdatnosti sportovců i běžné nesportující populace a nemocných.

 

HR (Heart Rate) - srdeční frekvence

je frekvence (dále jen jako SF), kterou se srdce stahuje - tepe; značí počet tepů udávaný obvykle za 1 minutu. SF bývá v klidu mezi 60–90 údery za minutu, u trénovaných osob sportovců bývá nižší.

 

HRR (Heart Rate Rest) - rezerva srdeční frekvence

slouží k posouzení rozdílu mezi srdeční frekvencí náležitou a skutečně naměřenou u pacienta při maximálně tolerované zátěži.

 

RQ (Respiratory Quotient) - respirační kvocient

je poměr udávající objem vydýchaného oxidu uhličitého na 1 litr vdechnutého kyslíku (CO2/O2). Dává informaci o složení energetických zdrojů v potravě. Běžně se pohybuje od 1,0 při čistě sacharidové stravě až k 0,7 při stravě čistě tukové, při smíšené stravě je hodnota kolem 0,85. Hodnota respiračního kvocientu je tím nižší, čím méně kyslíku živiny obsahují.

RER (Respiratory Exchange Ratio) - poměr výměny plynů

stanovuje, zdali v organismu dochází k energetickému krytí převážně v aerobní či anaerobní rovině.

RER = V (CO2) / V (O2).

 

Výběr parametrů byl dán účelem studie - jedná se o studii zaměřenou na hodnocení metabolického výdeje při zátěži, proto jsme z nabídky měřených parametrů Oxycon mobile vybrali právě parametry prokazující vliv na metabolismus člověka, spíše než ostatní - např. poukazující spíše na fyzickou zdatnost člověka (jako např. W/kg; V(O2) aj.

Tato pilotní studie je předběžnou studií v malém měřítku (v našem případě provedená na 30 probandech) konaná před hlavním výzkumem za účelem ověření proveditelnosti nebo vylepšení plánu výzkumu. Provádíme ji za účelem ověření správnosti námi navrženého hlavního projektu ve snaze ušetřit čas a náklady za nesprávně navržený projekt, k otestování návrhu hlavního experimentu.

 

Statistická analýza dat

Základní hypotéza (předpoklad):

Tříměsíční trénink nesportovce prokazatelně zlepší jeho metabolickou odezvu, přičemž není možné prokázat, jestli je jeden typ tréninku vhodnější než druhý.

K ověření základní hypotézy jsme vybrali celkem 5 parametrů, u nichž budeme zkoumat, jak (a zdali) se změnily jejich hodnoty po tříměsíčním tréninku.

Parametr MET

Přehled měřených hodnot parametru MET na začátku:

Tab. 3 MET měření

 

Tab. 4 Průměrné hodnoty

Graf 8 Histogramy naměřených hodnot:

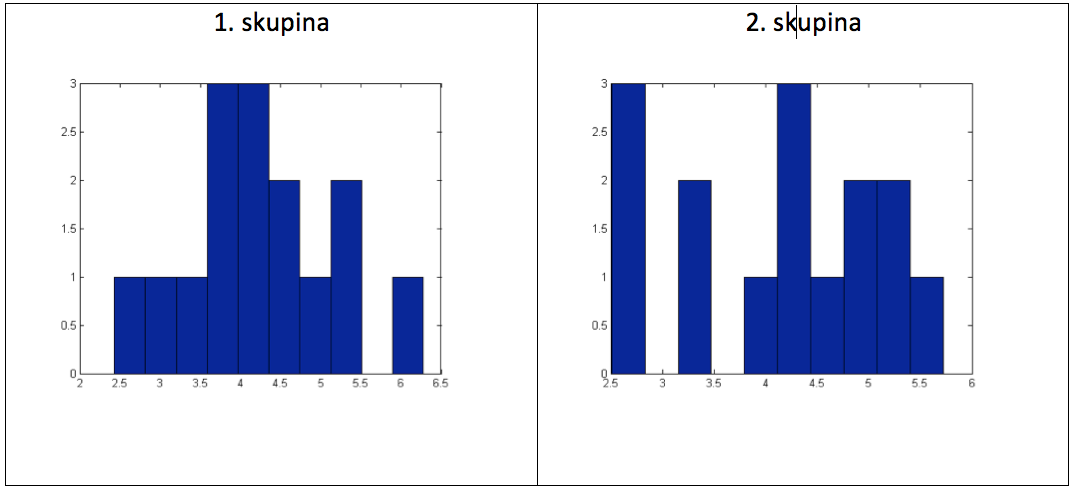
Před provedením statistických testů musíme zjistit, zda jsou naše data normálně rozdělena a zda tedy můžeme použít parametrické metody (předpokládající takové rozdělení). Pokud by data normálně rozdělena nebyla, museli bychom je buď transformovat nebo použít neparametrické metody.

Využitím Kolmogorovova-Smirnovova testu (případně Jarque-Bera či Lilliefors testu) v Matlabu (funkce kstest, jbtest, lillietest) ověříme normalitu dat. Každý z testů na hladině významnosti α=0,05 skončí s výsledkem, že není možné zamítnout nulovou hypotézu vyjadřující normální rozdělení dat.  Podle stránek výrobce Matlabu (www.mathworks.com) je pro malé vzorky nejvhodnější Lilliefors test. Ten dosáhne následujících hodnot:

1. skupina: p-hodnota: 0,451;   k-statistika: 0,152;  kritická hodnota testu: 0,219

2. skupina: p-hodnota: 0,500;   k-statistika: 0,113;  kritická hodnota testu: 0,219

Dále proto budeme předpokládat, že data jsou normálně rozdělena. Ještě ověříme, že data neobsahují odlehlé hodnoty (které bychom jinak museli odstranit).

Než vyhodnotíme vliv tréninku, zjistíme, jestli je na začátku nějaký rozdíl mezi skupinami. Jinak řečeno, bude nás zajímat, jestli se liší střední hodnoty parametru MET u sledovaných skupin.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením dvouvýběrového t-testu v Matlabu(funkce ttest2) při hladině významnosti  α=0,05 opět dospějeme k výsledku, že není možné zamítnout nulovou hypotézu.

p-hodnota: 0,791;   t-statistika: 0,268;  interval spolehlivosti: (-0,643;0,836); koeficient věcné významnosti ω²: -0,032 (tj. 0), přičemž

ω²=(t2-1)/(t2+n1+n2-1),

kde t=0,268 je t-statistika, n1=n2=15 jsou velikosti jednotlivých skupin.

Ze získaných hodnot usoudíme, že mezi skupinami není statisticky významný rozdíl. Statistická významnost není doprovázena věcnou významností. Pomocí programu Power and Sample Size zjistíme, že v případě síly testu 0,8 je statisticky prokazatelný rozdíl roven přibližně jedné. Předchozí výsledek můžeme chápat tak, že bylo statisticky prokázáno, že rozdíl ve středních hodnotách parametru MET mezi skupinami není větší než 1. Kdybychom například zvýšili počet žen ve skupině na 100, byl by statisticky prokazatelný rozdíl roven 0,4.

Naměřené hodnoty po 3 měsících:

Tab. 5 Měření po 3 měsících

Tab. 6 Průměry po 3 měsících

Graf 9 Histogramy naměřených hodnot

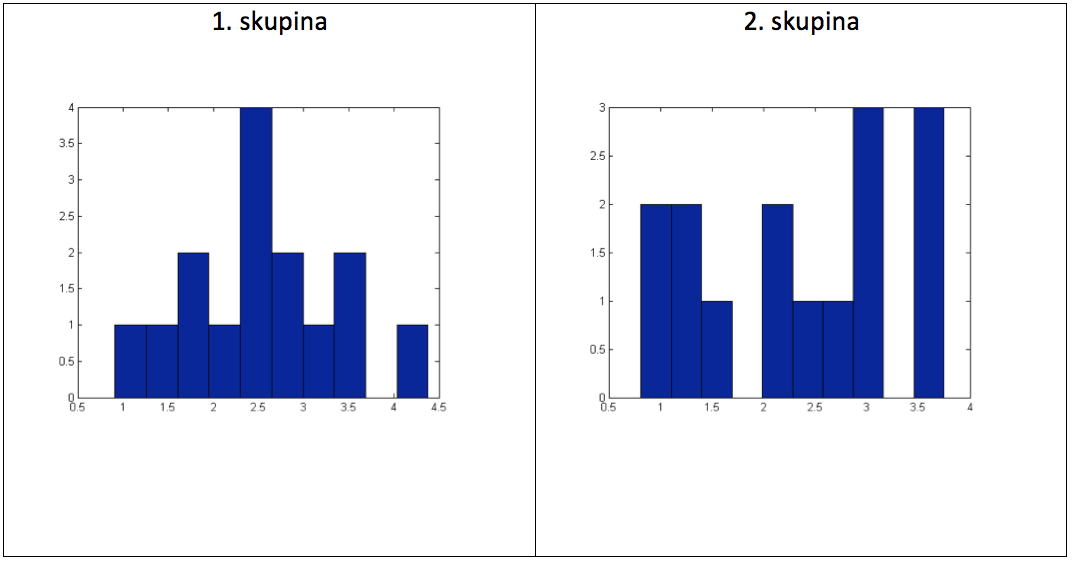
Po třech měsících tréninku chceme vědět, zda došlo k nějaké změně v měřeném parametru MET a zda se nyní nějak liší hodnoty obou skupin.

Nulová (testovaná) hypotéza H₀: rozdíl středních hodnot u první (resp. druhé) sledované skupiny je nulový.

Alternativní hypotéza H₁: rozdíl středních hodnot u první sledované skupiny není nulový.

Párový t-test (v Matlabu funkce ttest) provedený na hladině významnosti α=0,05 vede k zamítnutí nulové hypotézy (u obou skupin). Bylo přitom dosaženo hodnot:

1. skupina:

p-hodnota: 5*10-16; t-statistika: 40,825;  interval spolehlivosti: (1,628;1,809); koeficient věcné významnosti ω²: 0,982

2. skupina:

p-hodnota: 1*10-16; t-statistika: 46,291; interval spolehlivosti: (1,721;1,888); koeficient věcné významnosti ω²:  0,986

Statistická i věcná významnost si odpovídají. Můžeme proto konstatovat, že po třech měsících tréninku je prokázán rozdíl v naměřených hodnotách parametru MET. Doplňme, že před použitím párového t-testu bylo opět ověřeno, že data odpovídají normálnímu rozdělení a neobsahují odlehlé hodnoty (a t-test tedy mohl být proveden).

Nakonec zbývá zjistit, zda je nějaký rozdíl po tříměsíčním tréninku mezi sledovanými skupinami.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Nepárovým dvouvýběrovým t-testem (v Matlabu funkce ttest2) na hladině významnosti α=0,05 získáme týž výsledek jako před začátkem tréninku, který neumožňuje zamítnout nulovou hypotézu.

p-hodnota: 0,598; t-statistika: 0,534;  interval spolehlivosti: (-0,518;0,883); koeficient věcné významnosti ω²: -0,024 (tj. 0)

Ze získaných hodnot usoudíme, že mezi skupinami není statisticky významný rozdíl. Statistická významnost ovšem opět není doprovázena věcnou významností.

 Celkem jsme zjistili:

Po tříměsíčním tréninku je statisticky významný rozdíl v měřené hodnotě MET (a to u všech žen bez ohledu na druh tréninku). Naproti tomu se nepodařilo statisticky prokázat rozdíl mezi skupinami absolvujících různé druhy tréninku.

Parametr HR

Přehled měřených hodnot parametru HR na začátku:

Tab. 7 Parametry HR na začátku

Tab. 8 Průměry na začátku

Graf 10 Histogramy naměřených hodnot

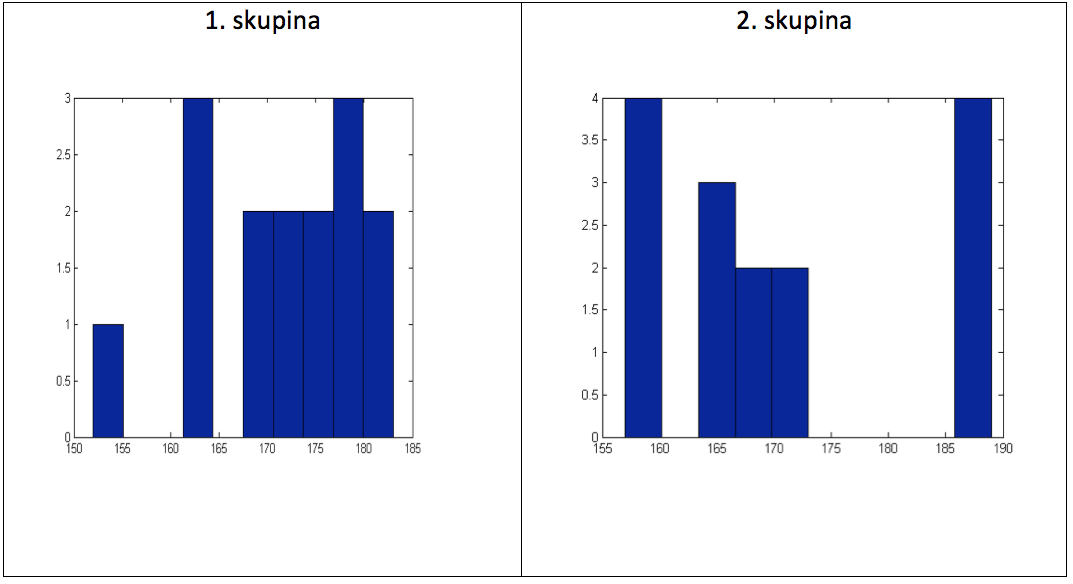
Postupovat budeme stejně jako u parametru MET. Nejprve tedy zjistíme (ověříme), zda jsou naměřené hodnoty normálně rozděleny. K tomu použijeme v Lilliefors test v Matlabu. Získáme následující hodnoty:

1. skupina: p-hodnota: 0,313;  k-statistika: 0,166; kritická hodnota testu: 0,219

2. skupina: p-hodnota: 0,153; k-statistika: 0,189; kritická hodnota testu: 0,219

Test sice skončil výsledkem, že není možné zamítnout nulovou hypotézu vyjadřující normální rozdělení dat, ovšem p-hodnota je v případě 2. skupiny hodnot velmi nízká a také z histogramu nabudeme podezření, že naše data nemají normální rozdělení.

Pro zjištění rozdílu mezi skupinami proto raději využijeme neparametrického Mann-Whitney testu, v Matlabu funkce ranksum.

Nulová (testovaná) hypotéza H₀: střední hodnoty jsou u sledovaných skupin shodné.   

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením Mann-Whitney testu na hladině významnosti 0,05 dospějeme k výsledku, že není možné zamítnout nulovou hypotézu, přičemž obdržíme následující hodnoty:

p-hodnota: 0,561; z-statistika: 0,582; součet pořadí (ranksum): 247

Naměřené hodnoty po 3 měsících:

Tab. 9 Hodnoty po 3 měsících

Tab. 10 Průměry po 3 měsících

Graf 11 Histogramy naměřených hodnot

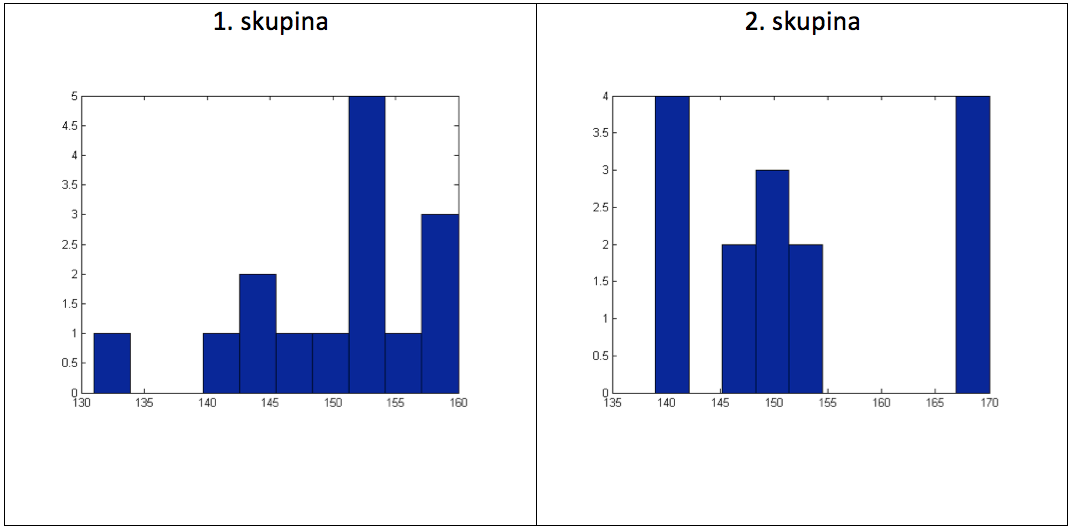
Pro posouzení existence rozdílu způsobeného tříměsíčním tréninkem provedeme u obou skupin párový neparametrický Wilcoxonův sign test na hladině významnosti 0,05, v Matlabu funkce signtest.

 Nulová (testovaná) hypotéza H₀: rozdíl středních hodnot u první (resp. druhé) sledované skupiny je nulový.

Alternativní hypotéza H₁: rozdíl středních hodnot u první sledované skupiny není nulový.

Pro obě skupiny dostaneme výsledek v podobě zamítnutí nulové hypotézy a hodnoty:

1. skupina: p-hodnota: 6*10-5; znaménková (sign)-statistika: 0

2. skupina: p-hodnota: 6*10-5; znaménková (sign)-statistika: 0

Ještě otestujeme, zda je po třech měsících (statisticky) nějaký rozdíl mezi skupinami. Opět k tomu využijeme neparametrický Mann-Whitney test.

Nulová (testovaná) hypotéza H₀: střední hodnoty jsou u sledovaných skupin shodné.        

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením testu na hladině významnosti 0,05 dospějeme k výsledku, že není možné zamítnout nulovou hypotézu, přičemž obdržíme následující hodnoty:

p-hodnota: 0,868;  z-statistika: 0,166;  součet pořadí (ranksum): 237

Celkem jsme zjistili:

Po tříměsíčním tréninku je statisticky významný rozdíl v hodnotě HR (a to u všech žen bez ohledu na druh tréninku). Naproti tomu se nepodařilo statisticky prokázat rozdíl mezi skupinami absolvujících různé druhy tréninku.

Parametr HRR

Přehled měřených hodnot parametru HRR na začátku:

Tab. 11 Hodnoty HRR na začátku

Tab. 12 Průměry HRR na začátku

Graf 12 Histogramy naměřených hodnot

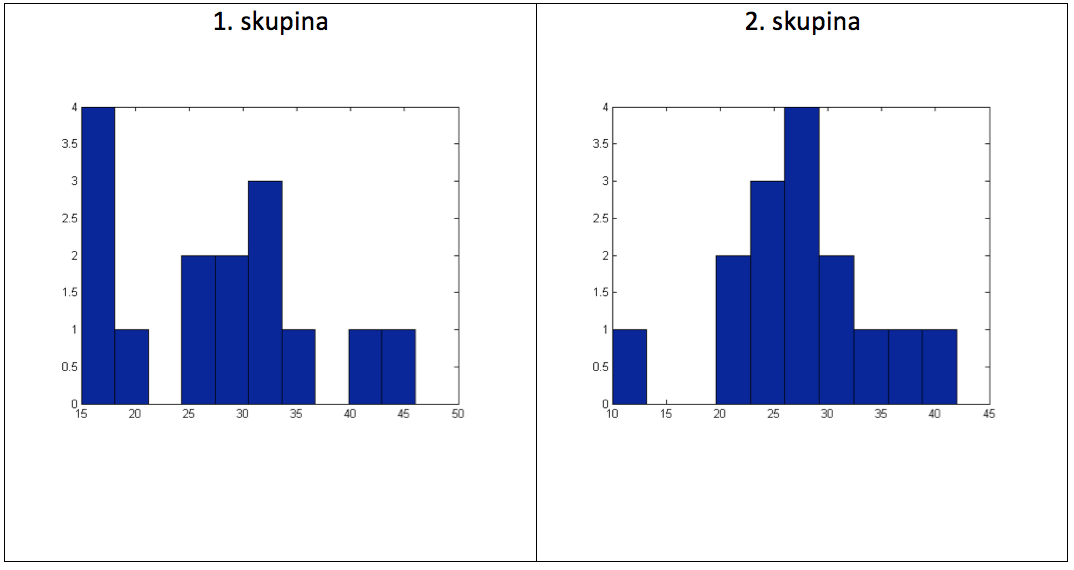
Použitím Lilliefors testu pro ověření normality dat získáme pro obě skupiny odpověď, že není možné zamítnout nulovou hypotézu (vyjadřující normalitu dat), a následující hodnoty:

1. skupina: p-hodnota: 0,500;   k-statistika: 0,123;  kritická hodnota testu: 0,219

2. skupina: p-hodnota: 0,308;   k-statistika: 0,167;  kritická hodnota testu: 0,219

I vzhledem k histogramům budeme tentokrát předpokládat, že jsou naměřená data normálně rozdělena a dále využívat parametrických t-testů.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením dvouvýběrového t-testu při hladině významnosti  α=0,05 opět dospějeme k výsledku, že není možné zamítnout nulovou hypotézu. Přitom obdržíme:

p-hodnota: 0,914; t-statistika: 0,109;  interval spolehlivosti: (-5,956;6,622); koeficient věcné významnosti ω²: -0,034 (tj. 0)

Podobně jako v prvním případě není statistická významnost podpořena věcnou významností. Pomocí programu Power and Sample Size opět můžeme zjistit, že v případě síly testu 0,8 je statisticky prokazatelný rozdíl roven přibližně třem. To znamená, že nemůžeme vyloučit, že mezi středními hodnotami skupin není menší rozdíl než 3. Pro vyšší „přesnost“ by byl potřeba větší vzorek (více žen ve skupině).

 Naměřené hodnoty po 3 měsících:

Tab. 13 HRR po 3 měsících

Tab. 14 Průměry HRR po 3 měsících

Graf 13 Histogramy naměřených hodnot

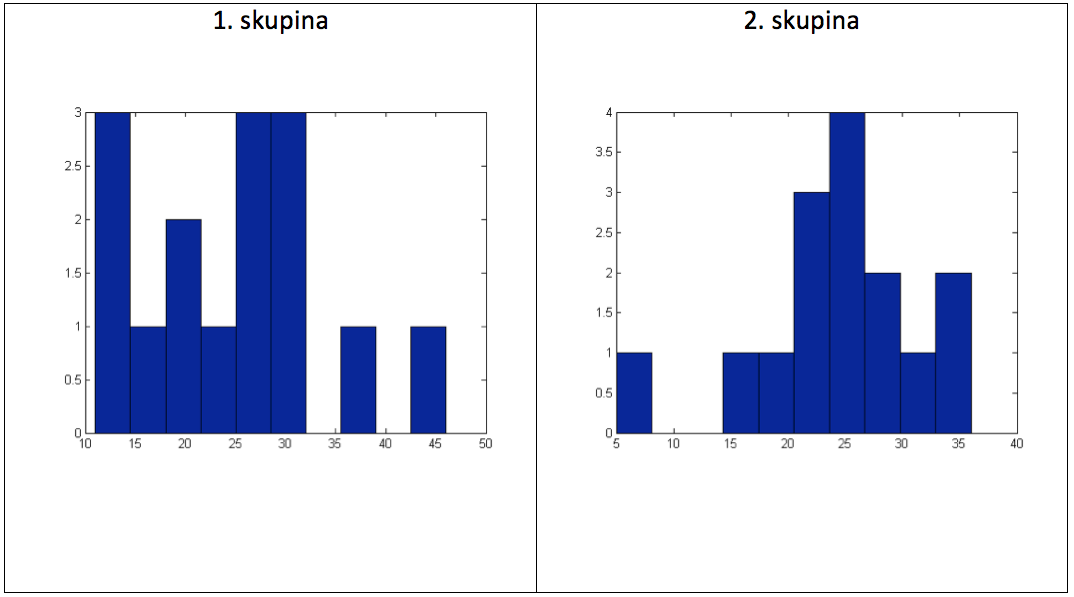
Po třech měsících tréninku chceme vědět, zda došlo k nějaké změně v měřeném parametru HRR a zda se nyní nějak liší hodnoty obou skupin.

Nulová (testovaná) hypotéza H₀: rozdíl středních hodnot u první (resp. druhé) sledované skupiny je nulový.

Alternativní hypotéza H₁: rozdíl středních hodnot u první sledované skupiny není nulový.

Párový t-test provedený na hladině významnosti α=0,05 vede k zamítnutí nulové hypotézy (u obou skupin). Bylo přitom dosaženo hodnot:

1.skupina: p-hodnota: 9*10-6 ; t-statistika: 6,782; interval spolehlivosti: (2,097;4,036); koeficient věcné významnosti ω²: 0,600

2. skupina: p-hodnota: 9*10-6 ; t-statistika: 6,782; interval spolehlivosti: (2,097;4,036); koeficient věcné významnosti ω²:  0,600

Statistická i věcná významnost si odpovídají. Můžeme proto konstatovat, že po třech měsících tréninku je prokázán rozdíl v naměřených hodnotách parametru HRR. Doplňme, že před použitím párového t-testu bylo opět ověřeno, že data odpovídají normálnímu rozdělení a neobsahují odlehlé hodnoty (a t-test tedy mohl být proveden).

Nakonec zbývá zjistit, zda je nějaký rozdíl po tříměsíčním tréninku mezi sledovanými skupinami.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Nepárovým dvouvýběrovým t-testem (v Matlabu funkce ttest2) na hladině významnosti α=0,05 získáme týž výsledek jako před začátkem tréninku, který neumožňuje zamítnout nulovou hypotézu.

p-hodnota: 0,919; t-statistika: 0,103;  interval spolehlivosti: (-6,324;6,991); koeficient věcné významnosti ω²: -0,034 (tj. 0)

Ze získaných hodnot usoudíme, že mezi skupinami není statisticky významný rozdíl. Statistická významnost ovšem opět není doprovázena věcnou významností.

Celkem jsme zjistili: Po tříměsíčním tréninku je statisticky významný rozdíl v měřené hodnotě HRR (a to u všech žen bez ohledu na druh tréninku). Naproti tomu se nepodařilo statisticky prokázat rozdíl mezi skupinami absolvujících různé druhy tréninku.

Parametr RQ

Přehled měřených hodnot parametru RQ na začátku:

Tab. 15 Hodnoty RQ na začátku

Tab. 16 Průměry RQ na začátku

Graf 14 Histogramy naměřených hodnot

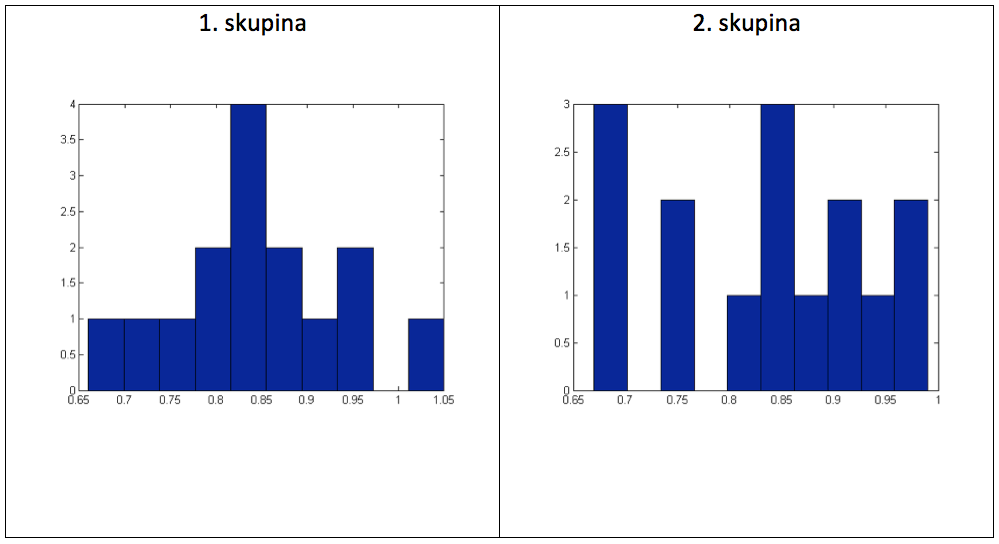
Použitím Lilliefors testu pro ověření normality dat získáme pro obě skupiny odpověď, že není možné zamítnout nulovou hypotézu (vyjadřující normalitu dat), a následující hodnoty:

1. skupina: p-hodnota: 0,305;   k-statistika: 0,167;  kritická hodnota testu: 0,219

2. skupina: p-hodnota: 0,500;   k-statistika: 0,118;  kritická hodnota testu: 0,219

Předpokládejme tedy, že data jsou normálně rozdělena. K dalšímu vyhodnocení využijeme parametrických t-testů.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením dvouvýběrového t-testu při hladině významnosti  α=0,05 opět dospějeme k výsledku, že není možné zamítnout nulovou hypotézu. Přitom obdržíme:

p-hodnota: 0,812; t-statistika: 0,240;  interval spolehlivosti: (-0,065;0,083); koeficient věcné významnosti ω²: -0,032 (tj. 0)

Podobně jako dříve není statistická významnost podpořena věcnou významností. Pomocí programu Power and Sample Size opět můžeme zjistit, že v případě síly testu 0,8 je statisticky prokazatelný rozdíl roven přibližně 0,1. To znamená, že nemůžeme vyloučit, že mezi středními hodnotami skupin není menší rozdíl než 0,1. Pro vyšší „přesnost“ by byl potřeba větší vzorek (více žen ve skupině).

Naměřené hodnoty po 3 měsících:

Tab. 17 RQ hodnoty po 3 měsících

Tab. 18 Průměry RQ po 3 měsících

Graf 15 Histogramy naměřených hodnot

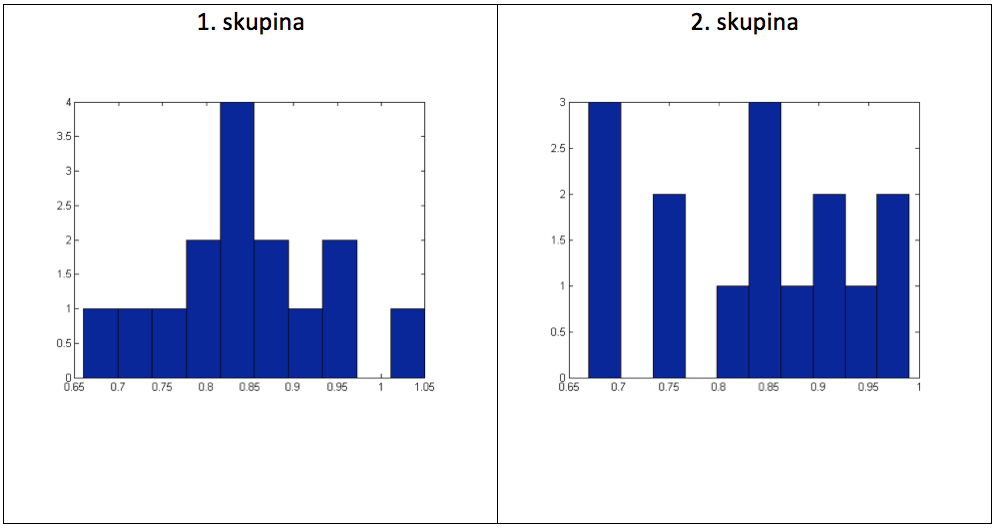
Po třech měsících tréninku chceme vědět, zda došlo k nějaké změně v měřeném parametru RQ a zda se nyní nějak liší hodnoty obou skupin.

Nulová (testovaná) hypotéza H₀: rozdíl středních hodnot u první (resp. druhé) sledované skupiny je nulový.

Alternativní hypotéza H₁: rozdíl středních hodnot u první sledované skupiny není nulový.

Párový t-test provedený na hladině významnosti α=0,05 vede k zamítnutí nulové hypotézy (u obou skupin). Bylo přitom dosaženo hodnot:

1. skupina: p-hodnota: 7*10-6; t-statistika: 6,910; interval spolehlivosti: (0,023;0,043); koeficient věcné významnosti ω²: 0,609

2. skupina: p-hodnota: 7*10-6; t-statistika: 6,910; interval spolehlivosti: (0,023;0,043); koeficient věcné významnosti ω²: 0,609

Statistická i věcná významnost si odpovídají. Můžeme proto konstatovat, že po třech měsících tréninku je prokázán rozdíl v naměřených hodnotách parametru RQ. Doplňme, že před použitím párového t-testu bylo opět ověřeno, že data odpovídají normálnímu rozdělení a neobsahují odlehlé hodnoty (a t-test tedy mohl být proveden).

Nakonec zbývá zjistit, zda je nějaký rozdíl po tříměsíčním tréninku mezi sledovanými skupinami.

Nulová (testovaná) hypotéza H₀: střední hodnoty a rozptyly jsou u sledovaných skupin shodné.

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Nepárovým dvouvýběrovým t-testem (v Matlabu funkce ttest2) na hladině významnosti α=0,05 získáme týž výsledek jako před začátkem tréninku, který neumožňuje zamítnout nulovou hypotézu.

p-hodnota: 0,819; t-statistika: 0,231;  interval spolehlivosti: (-0,068;0,085); koeficient věcné významnosti ω²: -0,033 (tj. 0)

Ze získaných hodnot usoudíme, že mezi skupinami není statisticky významný rozdíl. Statistická významnost ovšem opět není doprovázena věcnou významností.

 Celkem jsme zjistili:

Po tříměsíčním tréninku je statisticky významný rozdíl v měřené hodnotě RQ (a to u všech žen bez ohledu na druh tréninku). Naproti tomu se nepodařilo statisticky prokázat rozdíl mezi skupinami absolvujících různé druhy tréninku.

Parametr RER

Přehled měřených hodnot parametru RER na začátku:

Tab. 19 Naměřené hodnoty RER na začátku

Tab. 20 Průměry RER na začátku

Graf 16 Histogramy naměřených hodnot

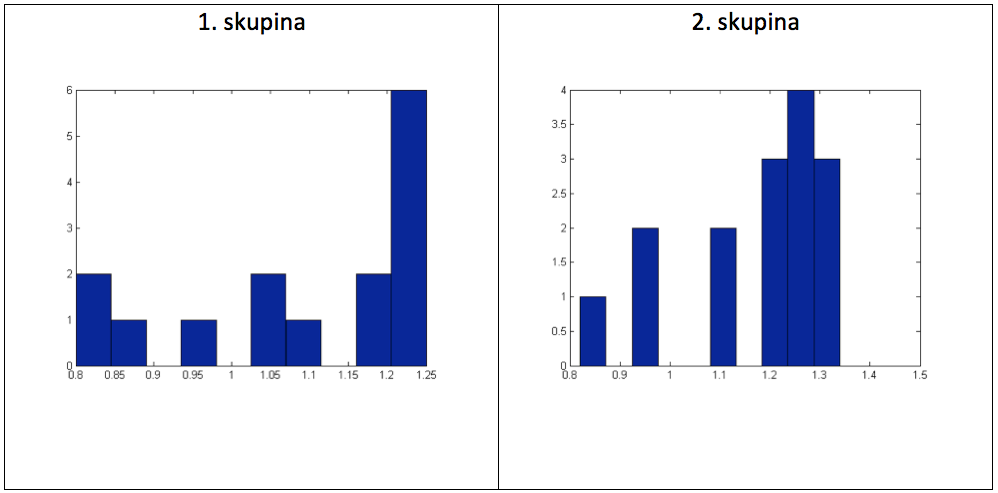
Použitím Lilliefors testu pro ověření normality dat získáme pro druhou skupinu odpověď zamítající nulovou hypotézu (vyjadřující normalitu dat), navíc v obou případech velmi nízké p-hodnoty:

1. skupina: p-hodnota: 0,058;   k-statistika: 0,215;  kritická hodnota testu: 0,219

2. skupina: p-hodnota: 0,005;   k-statistika: 0,267;  kritická hodnota testu: 0,219

V dalším proto budeme používat neparametrické testy.

Nulová (testovaná) hypotéza H₀: střední hodnoty jsou u sledovaných skupin shodné.        

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením Mann-Whitney testu na hladině významnosti 0,05 dospějeme k výsledku, že není možné zamítnout nulovou hypotézu, přičemž obdržíme následující hodnoty:

p-hodnota: 0,096;  z-statistika: -1,663;  součet pořadí (ranksum): 192

Vzhledem k p-hodnotě testu a popisným statistikám (průměr a směrodatná odchylka) nemůžeme vyloučit, že mezi skupinami není rozdíl (ve středních hodnotách).

Naměřené hodnoty po 3 měsících:

Tab. 21 Naměřené hodnoty RER po 3 měsících

Tab. 22 Průměry RER po 3 měsících

Graf 17 Histogramy naměřených hodnot

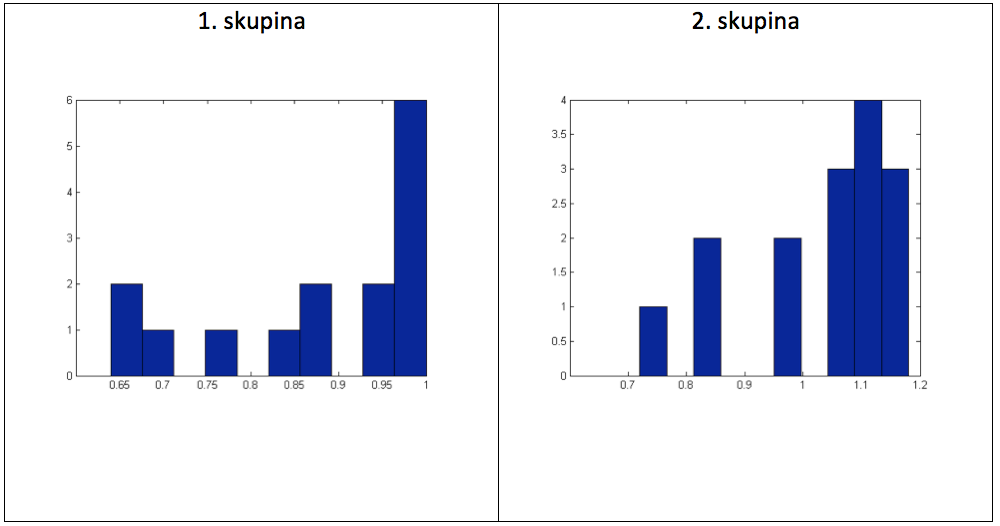
Pro posouzení existence rozdílu způsobeného tříměsíčním tréninkem provedeme u obou skupin párový neparametrický Wilcoxonův sign test na hladině významnosti 0,05.

Nulová (testovaná) hypotéza H₀: rozdíl středních hodnot u první (resp. druhé) sledované skupiny je nulový.

Alternativní hypotéza H₁: rozdíl středních hodnot u první sledované skupiny není nulový.

Pro obě skupiny dostaneme výsledek v podobě zamítnutí nulové hypotézy a hodnoty:

1. skupina: p-hodnota: 6*10-5; znaménková (sign)-statistika: 0

2. skupina: p-hodnota: 6*10-5; znaménková (sign)-statistika: 0

Ještě otestujeme, zda je po třech měsících (statisticky) nějaký rozdíl mezi skupinami. Opět k tomu využijeme neparametrický Mann-Whitney test.

Nulová (testovaná) hypotéza H₀: střední hodnoty jsou u sledovaných skupin shodné.        

Alternativní hypotéza H₁: střední hodnoty obou skupin jsou různé.

Provedením testu na hladině významnosti 0,05 dospějeme k výsledku zamítajícímu nulovou hypotézu (o stejných středních hodnotách obou skupin), přičemž obdržíme následující hodnoty:

p-hodnota: 0,004;  z-statistika: -2,885;  součet pořadí (ranksum): 162,5

Celkem jsme zjistili:

Po tříměsíčním tréninku je statisticky významný rozdíl v hodnotě RER (a to u všech žen bez ohledu na druh tréninku). Po tříměsíčním tréninku jsme navíc zaznamenali též rozdíl mezi skupinami, nemůžeme však vyloučit, že to bylo způsobeno rozdílností skupin již před započetím tréninku.

Vyhodnocení analýzy dat, shrnutí

U všech parametrů byl prokázán rozdíl způsobený tréninkem, všechny parametry byly vlivem tréninkového zatížení aerobního i anaerobního typu změněny. V parametru poměr respirační výměny byl prokázaný rozdíl mezi skupinami, což by poukazovalo na rozdílnou účinnost tréninkových jednotek, nicméně se nepodařilo prokázat, že mezi skupinami nevznikl a nebyl rozdíl již na začátku, tak není zřejmé, že konečný rozdíl byl způsobený tréninkem.

Diskuse

Nebyl prokázán rozdíl mezi testovanými skupinami. Z fyziologického pohledu je alespoň u určitých parametrů (poměr respirační výměny, respirační kvocient) nutno k hodnocení úspěšnosti projektu většího množství probandů, vedlo by to k posouzení významnosti rozdílů v naměřených hodnotách.

Námi vybraný vzorek 30 probandů může stačit k prokázání vlivu tréninku v obecné rovině, nicméně pro srovnání těchto dvou tréninkových procesů mezi sebou je zapotřebí větší testovací vzorek.