
Vyšetření variability srdeční frekvence (HRV) se stává široce používaným klinickým a výzkumným nástrojem. Analýza HRV navíc představuje zajímavou možnost pro vedení a kontrolu tréninkového zatížení. Avšak studií zabývajících se reliabilitou tohoto měření je stále nedostatek. Častou metodou hodnocení reliability měření HRV je metoda test-retest s opakováním měření po několika dnech až týdnech. Protože jsou výsledky měření HRV snadno ovlivnitelné nejrůznějšími vnitřními nebo vnějšími faktory, je podle našeho názoru vhodnější zopakovat měření okamžitě bez jakéhokoli přerušení (i tento způsob má ale své limity). Hlavním cílem předkládané studie bylo hodnocení absolutní a relativní reliability standardních ukazatelů HRV, získaných z krátkodobého laboratorního záznamu, který byl proveden v průběhu ortoklinostatického zatížení (Leh-Stoj-Leh). Cílem výzkumu bylo hodnocení absolutní a relativní reliability standardních ukazatelů HRV, získaných z krátkodobého laboratorního EKG záznamu, který byl proveden v průběhu ortoklinostatického zatížení (Leh-Stoj-Leh).
Měření může být nejen výzkumným nástrojem, ale také samo o sobě předmětem zkoumání. Přesnost a konzistence měření představují klíčový faktor. Získaná data, z kterých vyvozujeme určité závěry, musí být dostatečně validní a reliabilní. Právě reliabilita měření je ústředním tématem předkládané práce. Každé testování je vlastně měřením vlastnosti či kvality určitého subjektu a jako každé měření i toto může být „přesnější“ nebo „méně přesné“. Z tradičních důvodů se pro hodnocení přesnosti tohoto měření užívá tzv. reliabilita. [V odborné literatuře se používají i jiné ekvivalenty, např. opakovatelnost (angl. repeatability), reprodukovatelnost (angl. reproducibility), konzistence (angl. consistency), shoda (angl. agreement), konkordance (angl. concordance) nebo stabilita (angl. stability), (Atkinson & Nevill, 1998).] Reliabilitou rozumějme přesnost, konzistentnost měření, tj. schopnost dosáhnout stejného výsledku měření v případě, že se stav pozorovaného subjektu nezměnil.
Pojem „variabilita srdeční frekvence“ (HRV) je obecně akceptovaný název popisující oscilaci RR intervalů mezi po sobě následujícími srdečními stahy (Stejskal & Salinger, 1996). Vysoká HRV ukazuje na velkou adaptační kapacitu a je známkou zdravého jedince s dobře fungujícími autonomními kontrolními mechanismy. Naopak nízká HRV je často indikátorem abnormální a nedostatečné adaptability autonomního nervového systému (Pumprla et al., 2002).
Hlavním cílem předkládané studie bylo hodnocení absolutní a relativní reliability standardních ukazatelů HRV, získaných z krátkodobého laboratorního EKG záznamu, který byl proveden v průběhu ortoklinostatického zatížení (Leh – Stoj – Leh).
Metodika
Výzkumný postup
Předložená výzkumná práce se prostřednictvím opakovaného měření (test-retest) zabývá odhadem reliability (spolehlivosti) vyšetření kardiální autonomní regulace (KAR), které je realizováno ortoklinostatickou zkouškou. KAR byla hodnocena na základě analýzy HRV.
Samotné vyšetření HRV proběhlo vždy v ranních až dopoledních hodinách (7:30 – 10:00). Test se prováděl ve fyziologické laboratoři v Centru diagnostiky lidského pohybu (katedra tělesné výchovy, PedF, Ostravská univerzita). K vyšetření KAR pomocí analýzy HRV byl použit přístroj VarCor PF7 (Salinger & Gwozdziewicz, 2008; Salinger, Štěpáník, Krejčí & Stejskal, 2006).
Probandi byli poučeni o pravidlech vyšetření a nabádáni, aby dodrželi všechny standardní podmínky před testem, tzn. vyhnuli se intenzivnější pohybové aktivitě po dobu 48 h před vyšetřením, dostavili se nalačno a nepožili kofeinové nápoje. Alkoholické nápoje byly zakázány po dobu 24 h před vyšetřením. Kuřáci byli ze studie vyloučeni.
Zavedená podoba ortoklinostatické zkoušky se skládá ze tří intervalů: leh – stoj – leh. První poloha plní funkci standardizace a není využita k výpočtu jednotlivých parametrů. Z tohoto důvodu byla první poloha „leh“ u retestu odstraněna. Celý proces test-retest proto probíhal v pěti intervalech (tzn. leh-stoj-leh-stoj-leh).
Výzkumný soubor
Výzkumný soubor je tvořen 60 probandy (věk 22,3 ± 1,24; 60 mužů). Všichni jedinci byli v době měření bez akutních zdravotních obtíží a byli nekuřáci. Probandi byli studenty Ostravské univerzity a Vysoké školy báňské-TU Ostrava.
Analýza dat
Transformováním časových údajů o rozdílech mezi po sobě následujícími RR intervaly do frekvenčních hodnot získáváme výkonové spektrum. Analýza hustoty (denzity) spektrálního výkonu poskytuje informace, jak je tento výkon, který vyjadřuje velikost variability RR intervalů, rozložen v jednotlivých frekvenčních pásmech. Spektrální hustotu můžeme vypočítat pomocí rychlé Fourierovy transformace (FFT), která rozkládá vstupní signál na součet sinusových funkcí o různých frekvencích a amplitudách (Stejskal & Salinger, 1996).
Frekvenční rozsah „spektrálního obrazu“ a jednotlivých komponent je v této práci definován následovně:
- VLF („very lowfrequency“) – 0,02 až 0,05 Hz,
- LF („lowfrequency“) – 0,05 až 0,15 Hz,
- HF („highfrequency“) – 0,15 až 0,5 Hz (Stejskal & Salinger, 1996).
Výpočet spektrální výkonové hustoty (PSD) je prováděn podle částečně upraveného algoritmu CGSA (Yamamoto et al., 1991), který umožňuje optimální potlačení šumové složky analyzovaného signálu. Určení výsledné PSD [ms2.Hz-1] spočívá ve výpočtu rozdílu výkonové spektrální hustoty Sxx datového souboru x(t) a absolutní hodnoty vzájemné výkonové spektrální hustoty Sxysouborů x(t) a y(t) (Salinger et al., 1994):
PSD = Sxx – Sxy = F [x(t)] . F*[x(t)] – F [x(t)] . F* [y(t)]
x(t) - soubor hodnot RR intervalů analyzovaného úseku;
y(t) - pomocný soubor vytvořený zdvojením souboru x(t) pro výpočet podle algoritmu CGSA;
F[x(t)] - Fourierova transformace funkce x(t);
F*[x(t)] - komplexně sdružená Fourierova transformace funkce x(t);
F*[y(t)] - komplexně sdružená Fourierova transformace funkce y(t).
Spektrální výkon jednotlivých frekvenčních komponent (PVLF, PLF, PHF) udává velikost plochy (integrál) pod křivkou hustoty výkonového spektra. Celkový spektrální výkon (PT) je potom součtem spektrálních výkonů jednotlivých komponent. Velikost spektrálního výkonu může být vyjádřena také pomocí poměrových (VLF/HF, LF/HF, VLF/LF) a relativních (% VLF, % LF, % HF) ukazatelů. Koeficienty variace jednotlivých komponent kompenzují pokles spektrálního výkonu při zvýšení SF (Hayano et al., 1991).
V této práci jsou použity pro hodnocení reliability pouze nejčastěji se vyskytující parametry PT, PLF, PHF, LFnu, LF/HF.
Statistické zpracování dat
Za účelem řešení hlavního cíle předkládané studie byla srovnána párová data získaná v testu a retestu. Reliabilita měření byla hodnocena jako absolutní i relativní. Absolutní reliabilita je představována standardní chybou měření (SEM), která byla kalkulována podle Strauss et al. (2006). Dále byly spočítány 95% limity shody (LoA) (Bland & Altman, 1986). Relativní reliabilita byla hodnocena pomocí vnitrotřídního koeficientu korelace (ICC). Dále byla vypočítána velikost výzkumného souboru, která je potřebná k odhalení rozdílu výsledků ≥ 30 % směrodatné odchylky interindividuálních rozdílů. K hodnocení rozdílu průměru mezi skupinami párových dat byl použit párový t-test (α = 0,05).
Ze získaných dat bylo odstraněno odlehlé pozorování a byla kontrolována normalita distribuce dat (Kolmogův-Smirnovovův test, vizuálně dle P-P grafu) a případná heteroskedasticita (vizuálně dle Bland-Altmanova grafu) (ukázka viz grafy 1-7 pro PT v pozici leh).
Všechna data vykazovala porušenou normalitu rozdělení dat a přítomnost heteroskedasticity, a proto byla logaritmicky transformována.
Data byla statisticky zpracována pomocí počítačových programů Microsoft® Office Excel 2007 a IBM SPSS Statistics 20.
Výsledky
Významná změna průměru byla zaznamenána pouze u těchto parametrů v pozici Stoj: PT, PHF, PLF. Opakované měření bylo díky náhodné chybě v nejlepším případě 0.82–1.27krát (LFnu, STOJ) a v nejhorším případě 0.15–5.88krát (LF/HF, LEH) větší než první měření. ICC byl vždy větší než 0.7 (0.71–0.86). Odhadnutá potřebná velikost souboru se nacházela v rozmezí 16–33 jedinců (Tabulka 1).
Tabulka 1 Výsledky hodnocení reliability HRV parametrů
Vysvětlivky: HRV – variabilita srdeční frekvence, SEM – standardní chyba měření, LoA – limity shody, CI – interval spolehlivosti.
|
HRV parametr |
SEM |
95 % LoA |
ICC (95 % CI) |
Detekovaná změna a potřebná velikost souboru (n) |
t-test |
|
STOJ |
|||||
|
PT ln |
0.35 ln ms2 |
0.53, 3.72 |
0.78 (0.66-0.86) |
0.36 ln ms2 (n = 18) |
0.000 |
|
PHF ln |
0.38 ln ms2 |
0.44, 3.67 |
0.83 (0.73-0.89) |
0.41 ln ms2 (n = 16) |
0.001 |
|
PLF ln |
0.40 ln ms2 |
0.48, 4.43 |
0.78 (0.66-0.86) |
0.41 ln ms2 (n = 18) |
0.000 |
|
LF/HF ln |
0.41 ln |
0.36, 3.58 |
0.75 (0.61-0.84) |
0.33 ln (n = 27) |
0.098 |
|
LFnu ln |
0.08 ln |
0.82, 1.27 |
0.85 (0.75-0.91) |
0.08 ln (n = 17) |
0.201 |
|
LEH |
|||||
|
PT ln |
0.35 ln ms2 |
0.40, 2.88 |
0.85 (0.77-0.91) |
0.38 ln ms2 (n = 16) |
0.260 |
|
PHF ln |
0.39 ln ms2 |
0.37, 3.29 |
0.86 (0.77-0.91) |
0.43 ln ms2 (n = 16) |
0.183 |
|
PLF ln |
0.60 ln ms2 |
0.19, 5.51 |
0.76 (0.63-0.85) |
0.49 ln ms2 (n = 27) |
0.789 |
|
LF/HF ln |
0.55 ln |
0.15, 5.88 |
0.77 (0.63-0.87) |
0.46 ln (n = 25) |
0.826 |
|
LFnu ln |
0.50 ln |
0.23, 3.78 |
0.71 (0.55-0.81) |
0.36 ln (n = 33) |
0.496 |
Graf 4 Blandův-Altmanův graf pro rozdíl mezi prvním a druhým měřením

Rozložení jednotlivých bodů kolem nulové osy není symetrické (porušení normality rozdělení dat), což indikuje systematickou chybu mezi testem a retestem. Navíc postupný nárůst rozptylu kolem stejné osy naznačuje přítomnost heteroskedasticity.
Graf 5 Blandův-Altmanův graf pro rozdíl mezi prvním a druhým měřením po logaritmické transformaci dat uvedených v Grafu 4
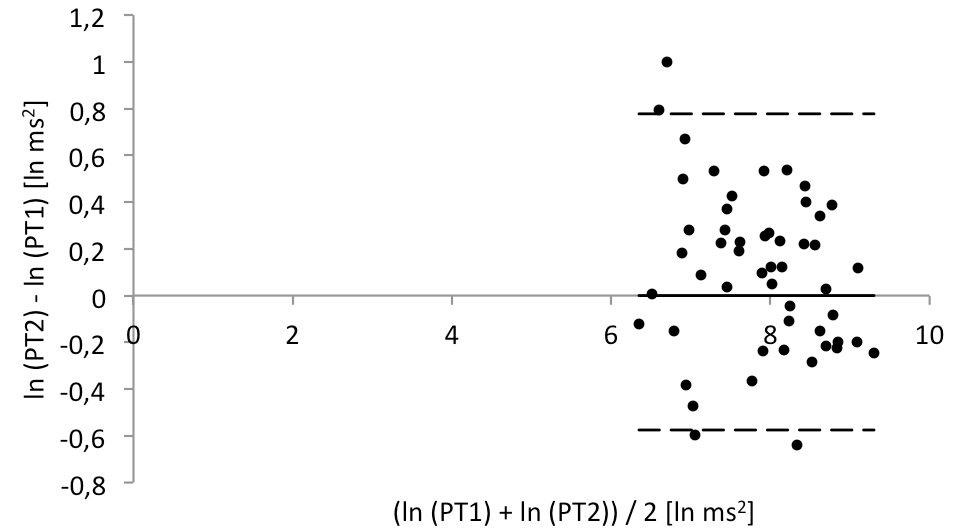
Rozložení jednotlivých bodů kolem nulové osy je symetrické, což indikuje absenci systematické chyby a také již můžeme konstatovat homoskedasticitu dat.
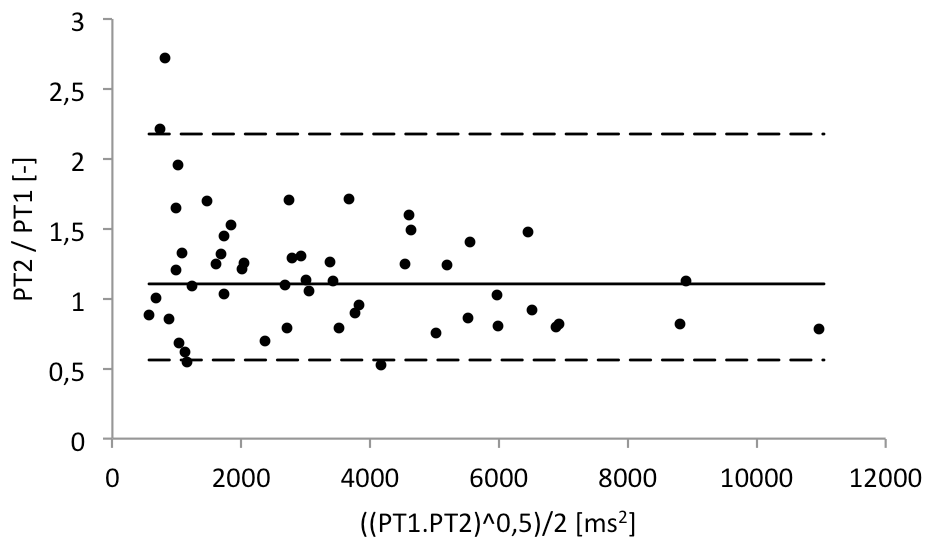
Graf 6 Blandův-Altmanův graf pro podíl druhého a prvního měření po logaritmické transformaci (pro heteroskedasticitní data)
Graf 7 Korelační pole měření 1 a 2

Rostoucí rozptyl kolem osy ukazuje přítomnost heteroskedasticity. Body ležící nad/pod přímkou souvisejí s případy, kdy retest vykazoval vyšší/nižší hodnoty než původní test.
Graf 8 Korelační pole měření 1 a 2 po logaritmické transformaci

Data lze po logaritmické transformaci považovat za homoskedasticitní. Body ležící nad/pod přímkou souvisí s případy, kdy retest vykazoval vyšší/nižší hodnoty než původní test.
Graf 9 P-P graf
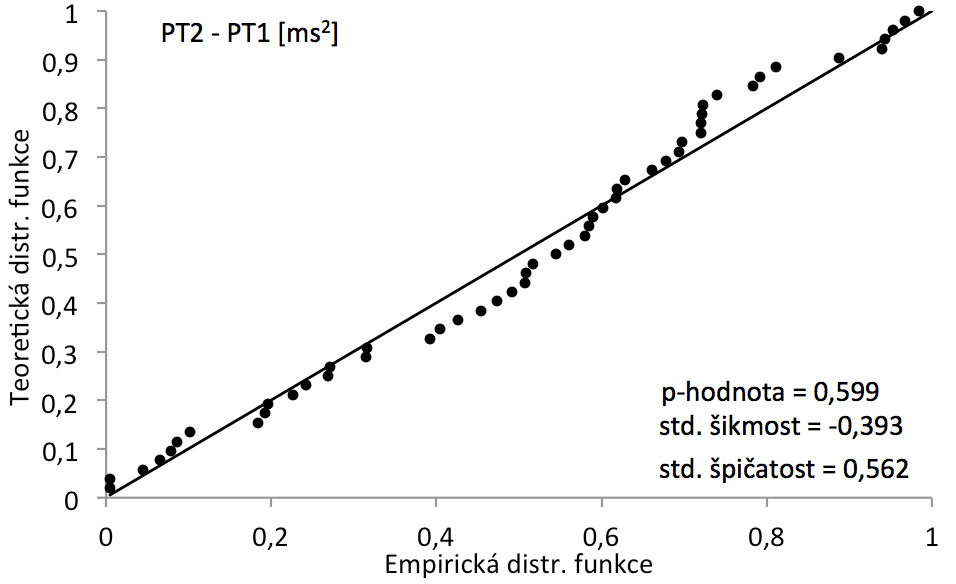
P-P graf pro PT2 - PT1 [ms2], p-hodnota pro test normality založený na šikmosti a špičatosti.
Na základě p-hodnoty není odchylka od normality statisticky významná (α = 0,05).
Graf 10 P-P graf pro logaritmicky transformovaná data
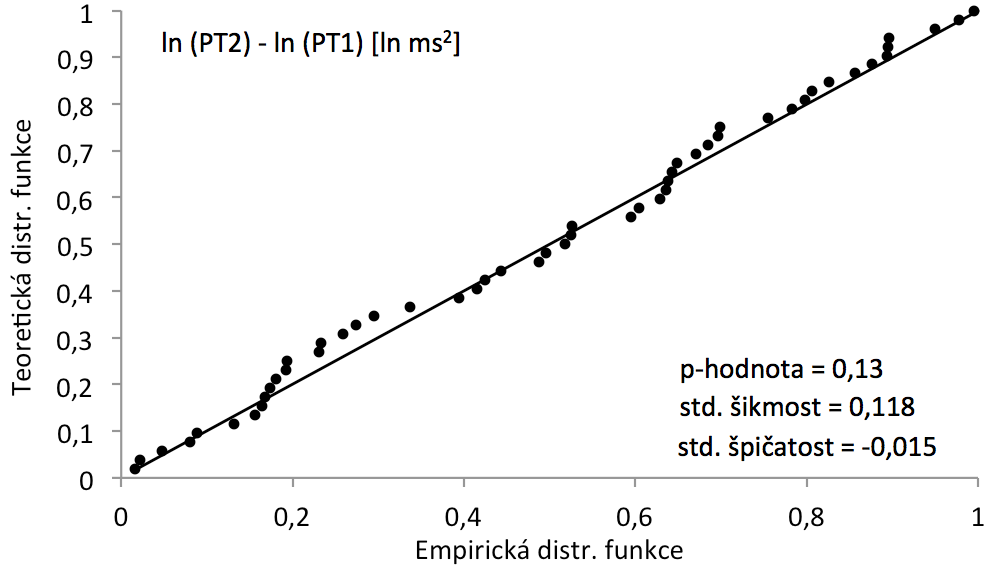
P-P graf pro ln (PT2) - ln (PT1) [ln ms2], p-hodnota pro test normality založený na šikmosti a špičatosti.
Transformace dat zmenšila odklon dat od přímky. Na základě p-hodnoty není odchylka od normality statisticky významná (α = 0,05).
Diskuze
Navzdory značnému počtu fyziologických a klinických výzkumů není reliabilita měření HRV stále jednoznačně potvrzena. Krátkodobé měření HRV je považováno za dostatečně stabilní například v práci autorů Sinnreich, Kark, Friedlander, Sapoznikov a Luria (1998). Zde se zároveň píše, že opakovatelnost výsledků komponent LF a HF se jeví větší než komponenty VLF. Avšak i VLF je dostatečně stabilní. Tarkiainen, Timonen a Tiittanen (2005) uvádějí, že největší stability v čase dosahují parametry průměrný RR interval a celkový spektrální výkon. Měření HRV je považováno za reliabilní ve studiích autorů Amara a Wolfe (1998), Cloarec-Blanchard, Funck-Brentano, Lipski, Jaillon a Macquin-Mavier (1997), Marks a Lightfoot (1999) nebo Parati et al. (2001). Také autoři Jauregui-Renaud et al. (2001) přišli k závěru, že opakovatelnost měření HRV u jednoho probanda byla větší než 95 %. Avšak koeficienty opakovatelnosti ukazovaly v této studii velké rozdíly mezi jednotlivými probandy. Proto nedoporučují používat výsledky HRV k interpretaci reakce na použitý test kardiovaskulárního reflexu ve skupině zdravých lidí. Pinna et al. (2007) navíc uvádí, že řízené dýchání zvyšuje reliabilitu měření HRV.
Na druhé straně existuje početná skupina studií, která odmítá jednoznačnou spolehlivost krátkodobého měření HRV (Bootsma, Swenne, & Bruschke, 1996; Freed, Stein, Gordon, Urban, & Kligfield, 1994; Lord et al., 2001; Piepoli et al., 1996; Ponikowski et al., 1996; Toyry, Mantysaari, Hartikainen, & Lansimies, 1995). Podle Pitzalis et al. (1996) je opakovatelnost parametrů frekvenční domény závislá na podmínkách, které jsou předmětem zkoumání daného výzkumu (např. použití léků nebo jiných intervencí ovlivňujících HRV). Negativní postoje k reliabilitě krátkodobého měření HRV se nejčastěji vyskytují u výzkumných souborů, které se skládají z probandů trpících různým onemocněním. Lord et al. to vysvětlují tím, že právě u těchto nemocných bývá HRV redukovaná, tzn. veškeré hodnoty získané z měření HRV jsou nižší, a proto i malé změny ve výsledcích test-retest mohou značně ovlivnit koeficienty validity a reliability. Sandercock et al. (2005) tvrdí, že popisovat měření HRV jako reliabilní by bylo přílišným zjednodušením, protože výsledky výzkumů reliability měření HRV závisí na mnoha faktorech.
Stanovení intraindividuálních rozdílů je nejdůležitější výsledek hodnocení reliability, protože ukazuje přesnost hodnocení změny proměnné v experimentální studii (Hopkins, 2000). V předkládané práci byla nalezena velká intraindividuální variabilita výsledků u všech hodnocených ukazatelů HRV. Hodnocení relativní reliability vychází z korelační analýzy. Tento bezrozměrný typ hodnocení naznačuje těsnost vztahu interindividuálních výsledků (Hopkins, 2000). Nízká absolutní reliabilita není v této studii zároveň doprovázená nízkou relativní reliabilitou. ICC byl vždy větší než 0,7 (0,71–0,86), což naznačuje dostatečnou relativní reliabilitu.
Shrnutí
Nalezena velká náhodná variace (intraindividuální) HRV parametrů (v pozici Leh i Stoj) musí být brána na zřetel ve výzkumných studiích. Navzdory nízké absolutní reliabilitě, náhodná chyba měření představuje pouze menší část celkové interindividuální variability, což představuje dobrou relativní reliabilitu. To znamená, že rozdíly mezi jedinci jsou způsobeny převážně opravdovými hodnotami, nikoli náhodnou chybou.
(brož. vaz., s. 28 - 44)