Porovnání klíčových kinematických veličin složitých přemetových a rondátových přeskoků v provedení vrcholových sportovních gymnastů

V kapitole je představena kinematická analýza složitých rondátových a přemetových skoků v provedení vrcholových gymnastů v závodě světového poháru s cílem porovnat techniku rondátových a přemetových skoků. Kapitola navazuje na předchozí kapitolu o technice provedení přemetu, analyzuje však větší vzorek vrcholných gymnastů přímo v reálném závodě.

Jedním z hlavních cílů výzkumu ve sportovní gymnastice je nalezení optimálního průběhu pohybové akce, aby bylo dosaženo co nejvyššího sportovního výkonu (Farana & Vaverka, 2010), a také pochopení již existující sportovní techniky (Prassas, Kwon, & Sands, 2006). Pochopením biomechanických souvislostí v průběhu pohybu lze přispět ke splnění základních cílů sportovní biomechaniky – zlepšení techniky, zlepšení tréninku a prevence zranění (McGinnis, 2005). Přeskok je koordinačně složitý pohyb vykonávaný v krátkém časovém intervalu (včetně rozběhu méně než 10 sekund), za který lze postihnout celou strukturu pohybu (Kopřiva & Pavlík, 1984; Čuk & Karáczony, 2004; Farana & Vaverka, 2011a) a na rozdíl od ostatních nářadí je tvořen pouze jednou dovedností (Sands, Caine, & Borms, 2003; Prassas, Kwon, & Sands, 2006). Z tohoto důvodu je přeskok nejčastěji zkoumanou a nejlépe pochopitelnou disciplínou gymnastického víceboje (Prassas et al., 2006). Po olympijských hrách v roce 2000 došlo k revoluční změně v přeskokovém nářadí. Tradiční přeskokový kůň byl nahrazen moderním přeskokovým stolem. Přeskokový stůl byl světovou gymnastickou federací (FIG) představen s hlavním cílem zvýšit bezpečnost sportovců, bez výrazné změny charakteru této disciplíny (Irwin & Kerwin, 2009). Na druhou stranu má větší oporná plocha a nový tvar přeskokového stolu za následek změny v obtížnosti předváděných skoků (Rand, 2003). Například zvýšení doby trvání druhé letové fáze umožňuje sportovním gymnastům provést během zvoleného letu komplexnější akrobatické cvičební tvary, tím zvýšit obtížnost skoku a možnost získat vyšší bodové hodnocení (Bradshaw et al., 2010). V pravidlech mužské sportovní gymnastiky existuje pět základních skupin přeskoků: Přímé skoky, Skoky s dvojným obratem v první letové fázi, Přemety vpřed, Přemety s ¼ nebo ½ obratem, Přeskoky po rondátu (Yurchenko) i s celým obratem (o 360°) v první letové fázi (Federation Internationale de Gymnastique, 2009). Přemety vpřed a Přemety s ¼ nebo ½ obratem jsou v mužské sportovní gymnastice nejčastěji prováděné skoky a jsou nejčastěji předmětem výzkumu (např. Dillman, Cheetham, & Smith, 1985; Takei & Kim, 1990; Takei, Dunn, & Blucker, 2003; Takei, 2007). Většina studií vycházejících z vrcholových soutěží vznikla v době, kdy se skákalo přes tradiční přeskokové nářadí, starého přeskokového koně. V současné době nejsou známa komplexní biomechanická data o přeskocích při použití nového přeskokového stolu (Bradshaw et al., 2010). Sledování vývoje přeskokových dovedností na přeskokovém stole je pro tréninkovou praxi ve sportovní gymnastice důležité a je potřeba dalších studií, které se budou zabývat srovnáním a popisem techniky mezi skupinami přeskoků u vrcholových gymnastů (Irwin & Kerwin, 2009). V této studii jsme se zaměřili na analýzu dvou konkrétních skoků ze skupiny 3 (Přemet vpřed a salto vpřed toporně s obratem 540°) a ze skupiny 4 (Rondát a salto vzad toporně s obratem 720° – Akopian), které mají podle pravidel sportovní gymnastiky stejné výchozí hodnocení (známka D), a to 6.2 bodů (FIG, 2009). Otázkou je, zda provedení odpovídá z pohledu kinematických parametrů obtížnostní známce, která je dána hodnotou přiřazenou ke každému skoku.

CÍL STUDIE

Cílem studie je porovnání klíčových kinematických parametrů u dvou skupin složitých přemetových skoků a skoků Cukahara v provedení vrcholových sportovních gymnastů během závodu světového poháru.

Metody

Výzkumný soubor

Výzkumný soubor tvořilo třináct sportovních gymnastů vrcholové úrovně, kteří se zúčastnili závodu světového poháru GRAND PRIX OSTRAVA v roce 2010. Všichni účastníci byli členy reprezentačních družstev příslušných států. U sportovních gymnastů bylo analyzováno 5 skoků (n=5) ze skupiny 3 (přemety vpřed v první letové fázi a salta vpřed i s obraty kolem vertikální osy ve druhé letové fázi) a 5 skoků (n=5) ze skupiny 4 (přemety s ¼ nebo ½ obratem o 90°–180° v první letové fázi a salta vzad i s obraty kolem vertikální osy ve druhé letové fázi), které byly sborem rozhodčích hodnoceny nejvyšší výslednou známkou. Všechny skoky měly podle pravidel sportovní gymnastiky známku D 6,2 (FIG, 2009). Věk, tělesná výška a tělesná hmotnost gymnastů byly 21,4 ± 1,9 let, 167,8 ± 4,7 cm a 64,6 ± 4,5 kg.

Data o věku, tělesné výšce a tělesné hmotnosti byla získána z oficiálních internetových stránek světové gymnastické federace (www.fig-gymnastics.com).

Experimentální nastavení

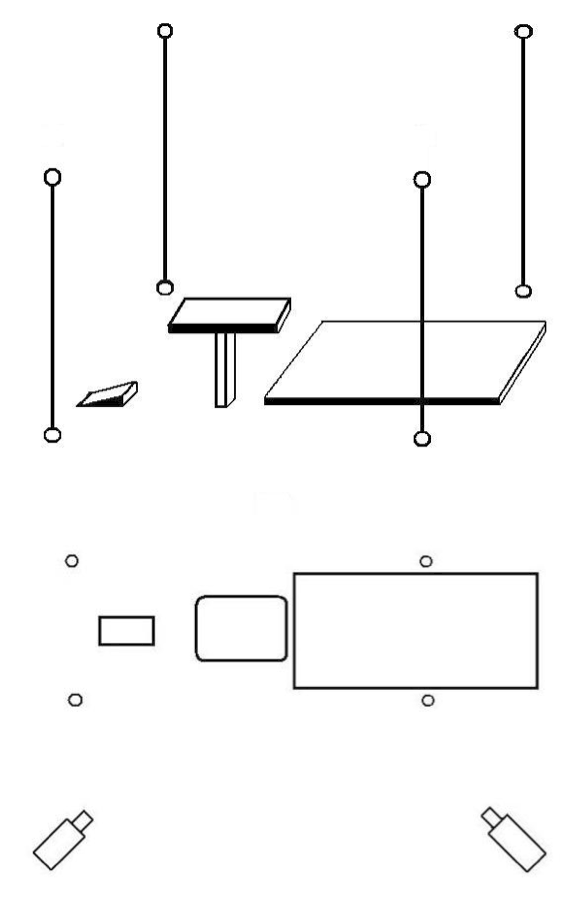
Základní metodou pro získání dat byla kinematografická (videografická) vyšetřovací metoda (Janura & Zahálka, 2004). Pro 3D analýzu pohybu byly použity dva digitální kamkordéry (Panasonic NV-MX500EG, Japan) se snímkovací frekvencí 50 půlsnímků/sek. Úhel mezi optickými osami kamer svíral přibližně 90°. Rychlost závěrek byla nastavena na 1/500. Obě kamery byly ve vzdálenosti přibližně 30 metrů od přeskokového nářadí (obr. 25). Kalibrovaný prostor byl ve čtyřech místech vymezen pomocí kalibrační tyče a tvořil virtuální kvádr o rozměrech 7×4×3 metry (obr. 26).

Obr. 25 Reálný snímaný prostor 3D analýzy ze dvou použitých kamer

Obr. 26 Grafické znázornění rozmístění kamer a vymezení kalibrovaného prostoru

Analýza dat

Získaná data byla digitalizována softwarem SIMI MOTION (SIMI Reality Motion Systems, Germany). Při digitalizaci záznamu bylo identifikováno 17 bodů: hlava, pravé rameno, pravý loket, pravé zápěstí, pravá ruka, pravá kyčel, pravé koleno, pravý kotník, pravá noha, levé rameno, levý loket, levé zápěstí, levá ruka, levá kyčel, levé koleno, levý kotník, levá noha. Pro určení polohy těžiště těla byl použit Gubitzův model (Gubitz, 1978). Pro každý analyzovaný skok bylo digitalizováno nejméně 75 snímků. Digitalizace začala pět snímků před kontaktem s odrazovým můstkem a končila pátým snímkem po dotyku doskokové žíněnky.

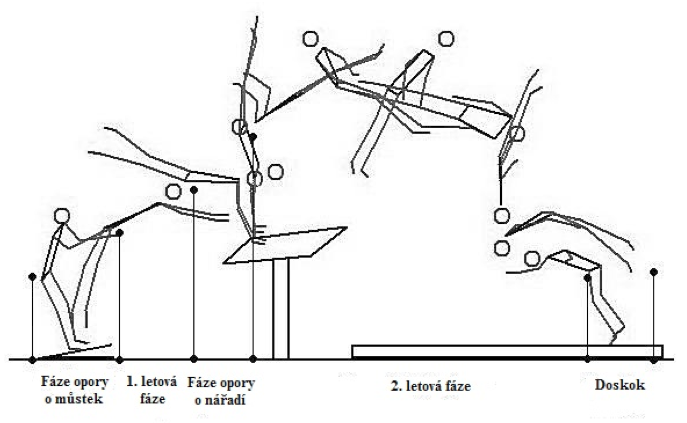
Doba trvání fáze opory o přeskokový můstek a přeskokový stůl byla určena jako čas od prvního snímku kontaktu gymnasty s odrazovým můstkem nebo přeskokovým stolem, po první snímek, kdy gymnasta ztratil kontakt s odrazovým můstkem nebo přeskokovým stolem. Doba trvání letové fáze byla určena jako čas od prvního snímku, kdy gymnasta ztratil kontakt s odrazovým můstkem nebo přeskokovým stolem, po první snímek kontaktu gymnasty s přeskokovým stolem nebo doskokovou žíněnkou (Takei et al., 2003). Z těchto kritických míst byly určeny jednotlivé fáze skoku: fáze opory o můstek, první letová fáze, fáze opory o nářadí, druhá letová fáze a fáze doskoku (obr. 27). Proměnné vertikální vzdálenosti těžiště těla byly určeny jako vzdálenosti těžiště těla od podložky v kritických fázích skoku. Horizontální vzdálenost těžiště těla v první letové fázi byla určena jako vzdálenost od místa odrazu z odrazového můstku po místo kontaktu s přeskokovým stolem. Horizontální vzdálenost těžiště druhé letové fáze byla určena jako vzdálenost od místa odrazu na přeskokovém stolu po místo kontaktu s doskokovou žíněnkou. Oficiální vzdálenost při doskoku byla určena jako vzdálenost od kraje přeskokového stolu po místo kontaktu s doskokovou žíněnkou.

Obr. 27 Stick figure diagram jednotlivých fází vybraného přeskoku

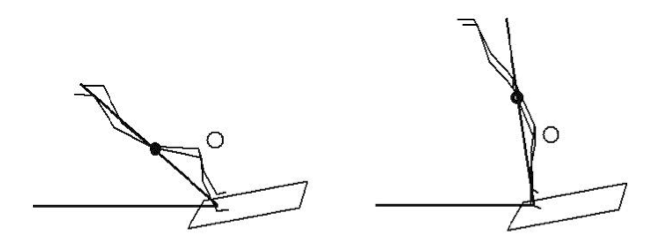
Úhel v místě kontaktu s přeskokovým nářadím byl definován jako úhel mezi vertikální osou procházející těžištěm těla a horizontální osou tvořenou přeskokovým stolem. Úhel při odrazu z přeskokového nářadí byl definován jako úhel mezi vertikální osou procházející těžištěm těla a horizontální osou tvořenou přeskokovým stolem (obr. 28).

Obr. 28 Stick figure diagram sledovaných úhlů ve fázi kontaktu a odrazu z přeskokového stolu (použito podle Farana & Vaverka, 2012)

Hrubá data byla vyhlazena použitím „low-pass“ filtru s mezní frekvencí 8 Hz (Bartlett, 2007). Chyba způsobená rozlišitelností záznamu měla hodnotu 0,013 m. To znamená, že posun kurzoru na monitoru o 1 pixel v horizontálním a vertikálním směru ve skutečnosti znamená posun vyhodnocovaného bodu o 1,3 cm. Pro určení velikosti celkové (subjektivní) chyby byl opakovaně digitalizován vybraný skok (Kerwin & Irwin, 2009). Velikost celkové (subjektivní) chyby byla určena pomocí opakované digitalizace vybraného skoku a měla hodnotu < 1 % pro časoprostorové parametry, < 4,5 % pro rychlostní parametry a < 3 % pro úhlové parametry. Časové, prostorové, rychlostní a úhlové parametry v klíčových fázích skoku byly vybrány a následně diskutovány na základě předchozích studií (Dilmann et al., 1985; Takei & Kim, 1990; Takei, 1998, 2007; Takei et al., 2003; Bradshaw et al., 2010), které řešily podobné problémy.

Statistické zpracování dat

Pro každou vyšetřovanou proměnnou byl určen aritmetický průměr a směrodatná odchylka (M ± SD) ze všech analyzovaných skoků.

Pro posouzení věcné významnosti rozdílů průměrů jsme vycházeli z odhadu koeficientu velikosti vlivu (ES), vyjádřený Cohenovým koeficientem (Cohen, 1988). Velikosti vlivu (ES) jsou vyjádřené jako 0–0,2 zanedbatelný efekt; 0,2–0,6 malý efekt; 0,6–1,2 střední efekt; 1,2–2,0 velký efekt; 2,0–4,0 velmi vysoký efekt a 4,0 a více excelentní (Hopkins, 2002). Efekt vyšší než 1,2 byl považován za věcně významný (Manning, Irwin, Gittoes & Kerwin, 2010).

Pro statistické zpracování dat byly použity softwary IBM SPSS Statistics 20 a Microsoft Excel.

Výsledky

Výsledky v tabulkách 17 a 18 ukazují rozdíly v kinematických proměnných u dvou vyšetřovaných skupin skoků.

Tabulka 17 Porovnání časoprostorových proměnných v jednotlivých fázích skoku mezi přemetovými skoky (n=5) a skoky Cukahara (n=5)

Legenda: M – průměr; SD – směrodatná odchylka; ES – Cohenův koeficient effect size; Efekt – slovní vyjádření síly efektu (Hopkins, 2002); s – sekunda; m – metr

U časových parametrů byl zjištěn velmi vysoký efekt v době trvání první letové fáze (ES=2,5) a ve fázi opory o přeskokový stůl (ES=3,9). Velký efekt byl zjištěn u doby trvání druhé letové fáze (ES=1,2). U prostorových parametrů byl zjištěn velmi vysoký efekt u horizontální vzdálenosti těžiště těla ve druhé letové fázi (ES=2,5). Velký efekt byl zjištěn u výšky těžiště těla ve fázi kontaktu s přeskokovým stolem (ES=1,7), horizontální vzdálenosti těžiště těla při první letové fázi (ES=1,3), výšky těžiště těla ve fázi odrazu z přeskokového stolu (ES=1,3) a maximální výšky těžiště těla během druhé letové fáze (ES=1,3; tab. 17).

U rychlostních parametrů byl zjištěn velký efekt u horizontální rychlosti těžiště těla ve fázi odrazu z můstku (ES=1,6). U úhlových parametrů byl velký efekt zjištěn u úhlu sklonu těla ve fázi kontaktu s přeskokovým nářadím (ES=1,4) a ve fázi odrazu z přeskokového stolu (ES=1,3; tab. 18).

Obr. 29 Porovnání průměrné dráhy těžiště těla v průběhu přemetových skoků a Cukahara skoků

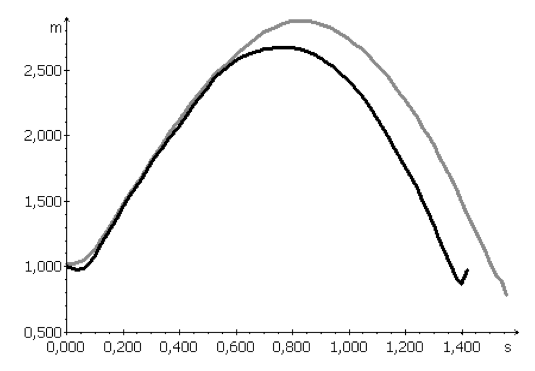
Legenda: Šedá linie zobrazuje průměrnou dráhu těžiště těla přemetových skoků (n=5). Černá linie zobrazuje průměrnou dráhu těžiště těla u skoků Cukahara (n=5).

Tabulka 18 Porovnání rychlostních a úhlových proměnných v jednotlivých fázích skoku mezi přemetovými skoky (n=5) a skoky Cukahara (n=5)

Legenda: M – průměr; SD – směrodatná odchylka; ES – Cohenův koeficient effect size; Efekt – slovní vyjádření síly efektu (Hopkins, 2002); m/s – metr za sekundu; ° – stupeň

Obr. 30 Porovnání průměrné horizontální rychlosti těžiště těla v průběhu přemetových skoků a Cukahara skoků

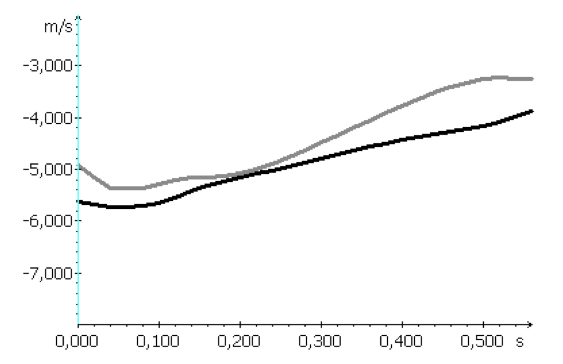
Legenda: Šedá linie zobrazuje průměrnou horizontální rychlost těžiště těla přemetových skoků (n=5). Černá linie zobrazuje průměrnou horizontální rychlost těžiště těla u skoků Cukahara (n=5).

Obr. 31 Porovnání průměrné vertikální rychlosti těžiště těla v průběhu přemetových skoků a Cukahara skoků

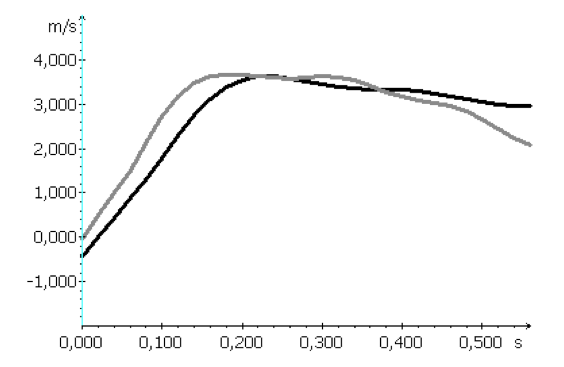
Legenda: Šedá linie zobrazuje průměrnou vertikální rychlost těžiště těla přemetových skoků (n=5). Černá linie zobrazuje průměrnou vertikální rychlost těžiště těla u skoků Cukahara (n=5).

Obr. 32 Porovnání průměrné výsledné rychlosti těžiště těla v průběhu přemetových skoků a Cukahara skoků

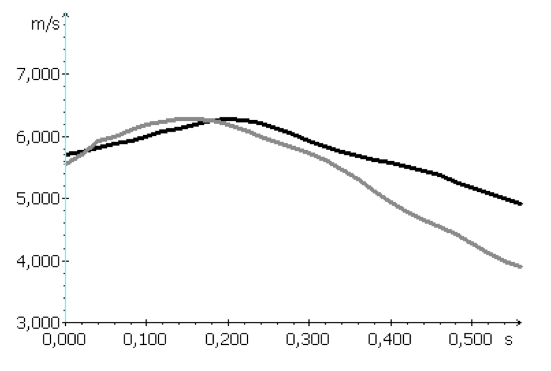
Legenda: Šedá linie zobrazuje průměrnou výslednou rychlost těžiště těla přemetových skoků (n=5). Černá linie zobrazuje průměrnou výslednou rychlost těžiště těla u skoků Cukahara (n=5).

Diskuse

K hodnocení věcné významnosti rozdílů průměrů jsme použili Cohenův index d. Jak uvádí Hendl (2009), je při posuzování velikosti účinku (effect size) nutné si uvědomit, že posouzení, který účinek lze považovat za velký, závisí na kontextu. Hranice navržené Cohenem (1988) a modifikované Hopkinsem (2002) jsou do jisté míry odůvodněné, ale nemají absolutní platnost.

U časových parametrů nebyl zjištěn rozdíl u doby trvání fáze opory na můstku (tab. 17). Bradshaw a Sparrow (2001) definují dynamicky provedený odraz krátkou dobou trvání kontaktu s odrazovým můstkem, která významně ovlivňuje dobu trvání druhé letové fáze. V naší studii dosahovali sportovní gymnasté kratší doby trvání opory o odrazový můstek než uvádí Takei et al. (2003) u přemetového skoku – přemet vpřed a dvojné salto vpřed skrčmo (FIG, 2009, 92) – a než uvádí Bradshaw et al., (2010) pro skok Cukahara toporně (FIG, 2009, 94) v provedení vrcholových sportovních gymnastů.

Velmi vysoký efekt byl zjištěn u doby trvání první letové fáze a opory o přeskokový stůl (tab. 17). V souladu s našimi výsledky uvádějí Čuk a Karácsony (2004), že se doba trvání a první letové fáze a fáze opory o přeskokové nářadí liší podle skupin skoků. V naší studii byla doba trvání první letové fáze kratší pro skoky Cukahara. To je zapříčiněno tím, že gymnasté dohmatají na přeskokový stůl střídmoruč, přičemž první dohmatová ruka dopadá na přeskokový stůl co nejrychleji po opuštění odrazového můstku. To je rovněž důvod, proč má fáze opory o přeskokové nářadí u skoků Cukahara delší časový průběh. Hodnoty časových parametrů u skoků Cukahara byly podobné těm, které uvádí Bradshaw et al. (2010). Nicméně byly zjištěny rozdíly v době trvání fáze opory o přeskokový stůl oproti studii Dillmann et al. (1985) o 0,07 s u skoků Cukahara a o 0,03 s u přemetových skoků. To naznačuje, že gymnasté v naší studii dokázali provést z přeskokového stolu více dynamický odraz než ti, kteří předvedli skoky přes tradičního přeskokového koně. Stejně jako u odrazu z můstku lze konstatovat, že u obou skupin skoků provedli sportovní gymnasté z naší studie z přeskokového stolu dynamický odraz (Bradshaw & Sparrow, 2001). Jak uvádí Bradshaw (2004) a Bradshaw et al. (2010), je pravděpodobné, že krátká doba kontaktu s přeskokovým stolem transformuje rozběhovou rychlost a rychlost při obou odrazech do delší doby trvání druhé letové fáze, vyšší výšky a delší vzdálenosti skoku. Tím je gymnastům umožněno provést ve druhé letové fázi komplexnější a složitější cvičební tvary.

V naší studii byl zjištěn velký efekt v době trvání druhé letové fáze, horizontální vzdálenosti první a druhé letové fáze, oficiální vzdálenosti při doskoku a maximální výšce během druhé letové fáze (tab. 17). Dohmat střídmoruč na přeskokový stůl při skocích Cukahara vede ke kratší horizontální vzdálenosti těžiště těla během první letové fáze. Odraz z přeskokového stolu je prováděn z jeho střední části a vede ke kratší horizontální vzdálenosti těžiště těla během druhé letové fáze. Naproti tomu u přemetových skoků je odraz prováděn z přední části přeskokového stolu a vede k delší horizontální vzdálenosti těžiště těla během druhé letové fáze. Přemetové skoky rovněž vyžadují zvětšit maximální výšku těžiště těla během druhé letové fáze a oficiální vzdálenost při doskoku (tab. 17). Rozdíly v časoprostorových parametrech během druhé letové fáze naznačují, že přemetové skoky vyžadují větší rozsah druhé letové fáze. Jak uvádí Takei (1998), je rozsah druhé letové fáze určen horizontální vzdáleností těžiště těla, maximální výškou těžiště těla, horizontální vzdáleností při doskoku a dobou trvání druhé letové fáze. Ačkoliv v naší studii obsahují skoky Cukahara během druhé letové fáze více obratů kolem vertikální osy otáčení, překvapivě vyžadují menší rozsah pohybu. To je pravděpodobně způsobeno tím, že gymnasta zahajuje obrat kolem vertikální osy otáčení již ve fázi odrazu z přeskokového stolu a využívá techniku obratů známou jako „contact twist“ (Yeadon, 1993a). Naproti tomu u přemetových skoků je obrat kolem vertikální osy otáčení zahájen až po odrazu z přeskokového stolu. Gymnasté tak využívají techniku obratů označovanou jako „aerial twist“, která je náročnější na rozsah pohybu během druhé letové fáze (Yeadon, 1993b).

U rychlostních parametrů byl zjištěn velký efekt u horizontální rychlosti těžiště těla při odrazu z můstku, přičemž vyšší rychlost byla zjištěna u skoků Cukahara. Nicméně nebyly zjištěny významné rozdíly ve výsledné rychlosti ve fázi odrazu z můstku. Zároveň nebyly zjištěny rozdíly ve všech rychlostních parametrech ve fázi kontaktu a odrazu s přeskokovým stolem (tab. 18). I přes rozdíly v době trvání kontaktu s přeskokovým stolem je zřejmé, že u obou skupin skoků je pro úspěšné provedení skoku nutná vysoká horizontální i vertikální rychlost ve fázi odrazu z přeskokového nářadí. Horizontální a vertikální rychlost při odrazu z můstku jsou rozhodující veličiny pro horizontální vzdálenost při doskoku, respektive pro výšku druhé letové fáze. Irwin a Kervin (2009) uvádějí, že jedním z účinků nového přeskokového nářadí ve srovnání s přeskokovým koněm je zvýšení vertikální rychlosti při odrazu z přeskokového stolu.

Velký efekt byl zjištěn u úhlu při kontaktu s přeskokovým stolem (tab. 18). Překvapivě byl u skoků Cukahara zjištěn větší úhel při kontaktu přeskokového stolu než u skoků přemetových. U obou skupin skoků byl odraz z přeskokového stolu dokončen před dosažením polohy stoje na rukou a nepřesáhl úhel odrazu 90° (Li, 1998). Li (1998) uvádí, že přesáhne-li úhel při odrazu 90°, ztrácí druhá letová fáze na vertikální výšce a horizontální vzdálenosti.

Shrnutí

Ačkoliv mají obě skupiny skoků podobné výchozí bodové hodnocení, jeví se přemetové skoky z pohledu biomechanické analýzy jako technicky náročnější. Z výsledků vyplývá, že přemetové skoky vyžadují větší rozsah druhé letové fáze, potřebný pro zahájení a dokončení rotačního pohybu a následný doskok. Z pohledu prevence zranění je proto u obou skupin skoků nutné maximalizovat rozsah druhé letové fáze, tím získává sportovní gymnasta dostatek času pro bezpečný a kontrolovaný doskok a předchází tak nebezpečí zranění v důsledku nedokončení rotačního pohybu během druhé letové fáze.