
Akrobatičtí skokané na lyžích se ve výskoku několikrát otočí kolem longitudinální a transverzální osy. Jak je možné, že v průběhu jednoho skoku dokážou své tělo s lyžemi takto roztočit, rotaci zrychlovat nebo zpomalovat a těsně před dopadem rotovat velmi pomalu? Jak gymnasté, krasobruslaři a další sportovci dokážou zvýšit a zase snížit rychlost rotace při akrobatických prvcích, přestože nejsou v kontaktu se zemí? Proč při hodu kladivem volí sportovci rotační techniku? Pokusíme se v této kapitole poskytnout teoretický základ pro odpovědi na podobné otázky.
Setrvačnost rotujících těles
Vlastnost těles odolávat změnám rotačního pohybu nazýváme setrvačnost rotujících těles. U těles, která mají více rotační setrvačnosti, je energeticky náročnější zvýšit nebo snížit úhlovou rychlost nebo změnit polohu osy rotace těchto těles. Plné kolo cyklisty, který jede sprint, bude odporovat pohybu při startu a naopak bude obtížnější ho zastavit na konci pohybu než kolo nevyplněné a tudíž lehčí. Jen lidé s výjimečnou rovnováhou jsou schopni stát s kolem na místě, zatímco při jízdě rovnováhu udrží většina lidí bez problémů. Všechny tyto jevy jsou dány setrvačností. Plné rotující kolo má větší setrvačnost, protože má větší hmotnost. Při rotaci navíc kolo odporuje změnám polohy osy otáčení, proto se nám dobře udržuje rovnováha při jízdě.
Míra setrvačnosti však není dána pouze hmotností těles, ale také tím, jak je hmotnost těles rozložena vůči ose rotace. Švih s delší golfovou holí je obtížnější než švih s holí kratší.
Moment setrvačnosti
Kvantitativní vyjádření míry setrvačnosti rotujícího tělesa je moment setrvačnosti:
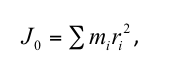
kde J0 (kg⋅m2) je moment setrvačnosti vůči ose, která prochází těžištěm, Σ sumační symbol, mi (kg) hmotnost i-tého elementu tělesa (např. segmentu lidského těla) a ri(m) vzdálenost i-tého elementu tělesa od osy otáčení procházející těžištěm.
Každý segment lidského těla odporuje změnám rotačního pohybu. Mírou odporu je součin hmotnosti segmentu a druhé mocniny vzdálenosti tohoto segmentu od osy otáčení, tedy moment setrvačnosti.
Zatímco setrvačnost lineárně se pohybujících těles je závislá pouze na jedné veličině (hmotnosti), setrvačnost rotujících těles je závislá na dvou veličinách (hmotnosti a vzdálenosti elementu od osy otáčení – charakteristika rozložení hmoty kolem osy otáčení). Tyto dvě veličiny nemají stejný vliv na moment setrvačnosti. Vliv hmotnosti na setrvačnost rotujících těles je mnohem menší než vliv rozložení hmoty. Dvojnásobné zvýšení hmotnosti zvýší moment setrvačnosti dvakrát, ale dvojnásobné zvýšení poloměru gyrace72 zečtyřnásobí moment setrvačnosti daného tělesa. Například délka pálky ovlivňuje při shodném technickém provedení a úsilí dobu potřebnou k odpálení projektilu (tenisový, pingpongový míč atd.) mnohem více, než její hmotnost.
Když používáme sportovní náčiní (pálky, rakety, hole a další), vytváříme takovou sílu, která otáčí náčiní kolem osy, která neprochází těžištěm těchto náčiní. Takovýto moment setrvačnosti je potom možné vypočítat takto:

J (kg·m2) je moment setrvačnosti vůči ose, která neprochází těžištěm, J0 (kg·m2) moment setrvačnosti vůči ose, která prochází těžištěm, m (kg) hmotnost tělesa (náčiní) a r (m) vzdálenost osy otáčení od k této ose rovnoběžné osy procházející těžištěm daného tělesa. To znamená, že moment setrvačnosti tělesa vůči ose, která neprochází těžištěm, je vždy větší, než moment setrvačnosti vůči ose, která těžištěm prochází a je s ní rovnoběžná.
Když budete ve sportovní praxi kvalitativně hodnotit odpor tělesa ke změně rotace, vzdálenost hmoty tělesa od osy rotace je nejdůležitější faktor ovlivňující setrvačnost daného rotujícího tělesa.
Každé těleso má nekonečně mnoho možných momentů setrvačnosti, protože může rotovat kolem nekonečně mnoha os otáčení.
V tělesné výchově a sportu většinou používáme tři hlavní osy k hodnocení pohybu. Hvězdu děláme v gymnastice kolem osy anteroposterior, salto kolem osy transverzální a otočku kolem osy longitudinální.
Záměrná změna momentu setrvačnosti lidského těla
Lidské tělo není tuhé těleso, protože se jednotlivé segmenty lidského těla mohou vůči sobě pohybovat. Z tohoto důvodu je moment setrvačnosti lidského těla vzhledem k jedné ose rotace proměnná veličina. To znamená, že můžeme moment setrvačnosti našeho těla záměrně měnit tak, aby byl pro nás výhodný pro dosažení lepšího sportovního výkonu nebo zvládnutí zadaného pohybového úkolu. Krasobruslař může více než zdvojnásobit svůj moment setrvačnosti kolem longitudinální osy, pokud provede abdukci horních končetin na úroveň ramene. Gymnasta může snížit při saltu moment setrvačnosti kolem transverzální osy až na polovinu, pokud se dostatečně těsně sbalí (obr. 23). Sprinter provádí flexi dolní končetiny v koleni a kyčli, když úhlově zrychluje dolní končetinu při švihu, čímž redukuje moment setrvačnosti dolní končetiny vzhledem k ose otáčení procházející kyčelním kloubem.
Obrázek 23 Gymnasta při provádění složitého přeskoku s dvojným saltem vpřed v poloze skrčmo ve druhé letové fázi - Roche vault. Gymnasta se při saltu sbalí tak, aby záměrně snížil moment setrvačnosti.

Gymnasté, krasobruslaři, atleti a mnoho dalších sportovců záměrně mění svůj moment setrvačnosti tak, aby vykonávali pohybové dovednosti efektivněji.
Výrobci sportovního náčiní a vybavení se také snaží vytvořit náčiní s takovým momentem setrvačnosti, aby byl co nejvýhodnější pro vykonání pohybové dovednosti. Sjezdaři používají delší lyže než slalomáři. Delší lyže poskytují lyžaři potřebnou stabilitu, když se pohybuje rychlostí přibližně 100 km/h. Slalomáři potřebují lyže, se kterými mohou rychle měnit směr, tedy lyže s menším momentem setrvačnosti kolem osy otáčení lyžaře. Slalomáři používají z tohoto důvodu kratší lyže. Výrobci některých slalomových lyží dokonce špičku lyže vyplňují lehčím materiálem, aby snížili její moment setrvačnosti.
Moment setrvačnosti a posuvná rychlost
Z předešlých kapitol víme, že když prodloužíme například hokejku, zapříčiníme tím větší rychlost na „lopatě“ hokejky, pokud jsme schopni hokejkou švihnout se stejnou úhlovou rychlostí. Puk potom poletí větší rychlostí. Proč tedy hokejisté nepoužívají například hokejky 2 m dlouhé? Naneštěstí, pokud prodloužíme hokejku, zvýšíme tím také moment setrvačnosti a úhlově zrychlit hokejku při švihu je potom mnohem těžší, protože je zapotřebí vynaložit více energie, tzn. vykonat větší práci. Hokejka tedy musí mít optimální délku tak, aby se s ní dalo střílet velkou rychlostí a zároveň překonávat co nejmenší setrvačný odpor. Vliv momentu setrvačnosti na rychlost se projevuje také u jiných náčiní, jako jsou golfové hole, tenisové rakety, pálky všeho druhu a jiné.
Moment hybnosti
Moment hybnosti L (kg·m/s) je definován jako součin momentu setrvačnosti J (kg·m2) vzhledem k ose otáčení a úhlové rychlosti ω (rad/s) rotujícího tělesa:

Jednotkou momentu hybnosti je kilogram metr za sekundu (kg·m/s). Moment hybnosti je vektor a má tedy velikost a směr. Směr momentu hybnosti je stejný jako směr úhlové rychlosti, která ho definuje.
Moment hybnosti tuhého tělesa
Moment hybnosti je závislý na dvou veličinách, momentu setrvačnosti a úhlové rychlosti. Pro dokonale tuhá tělesa změna momentu hybnosti závisí jen na jedné proměnné veličině a tou je úhlová rychlost, protože se moment setrvačnosti tuhých těles nemění73. U těles, která nejsou dokonale tuhá (lidské tělo) změna momentu hybnosti může být zapříčiněna jak změnou úhlové rychlosti, tak změnou momentu setrvačnosti.
Moment hybnosti lidského těla
Součet momentů hybností jednotlivých segmentů lidského těla nám dává přibližnou hodnotu momentu hybnosti celého těla74. Takže například během běhu se pravá horní končetina otáčí dopředu a levá horní končetina dozadu a stejně tak opačně vůči sobě se pohybují dolní končetiny. S ohledem na to, že moment hybnosti je vektor a záleží na směru otáčení daného segmentu kolem zvolené transverzální osy, moment hybnosti celého těla vzhledem k transverzální ose je nulový75.
Interpretace prvního Newtonova zákona pro otáčivý pohyb těles
Moment hybnosti daného tělesa zůstává konstantní, dokud na těleso nezačne působit nenulový výsledný vnější moment síly.
Pro sportovní praxi to znamená, že není možné započít otáčení lidského těla až po odrazu76. Proto gymnastičtí a akrobatičtí trenéři učí své svěřence, že již při odrazu musí způsobit rotaci jejich těla. První Newtonův zákon nám neříká, že by úhlová rychlost musela zůstat stejná, když nepůsobí žádný vnější moment síly. Proto se může po odrazu v průběhu skoku měnit úhlová rychlost těla, jestliže aktivně měníme jeho moment setrvačnosti. Úhlová rychlost lidského těla se potom mění tak, aby moment hybnosti po odrazu byl stále beze změny: L = Jω = konstantní . Když se například lyžař po nepovedeném skoku na muldě rozbalí, zvýší tím moment setrvačnosti svého těla vzhledem k ose otáčení, jeho úhlová rychlost otáčení se sníží tak, aby moment hybnosti zůstal stejný jako v momentě těsně po odrazu. Lyžař tak v okamžiku dopadu na sjezdovku může být v takové poloze, která mu umožní pokračovat v jízdě a udržet rovnováhu, aniž by dopadl na záda. Pokud člověk rotuje, může rychlost rotace ovlivňovat pohybem těla tak, že při sbalení hmoty těla blíže k ose otáčení bude rotovat rychleji a při přemístění hmoty těla dále od osy otáčení bude rotovat pomaleji při stejném momentu hybnosti77.
Dalším zcela typickým příkladem využití záměrné změny momentu setrvačnosti ve sportu je efekt změn rychlosti otáčení krasobruslaře při piruetě bez odrazu od země. Tření mezi ledem a bruslí je zanedbatelné a proto se krasobruslař po odraze může poměrně dlouho otáčet na jedné noze. Pokud má krasobruslař horní končetiny vzpaženy, jeho moment setrvačnosti je menší než v situaci, kdy jsou upaženy. Moment hybnosti je dán součinem úhlové rychlosti a momentu setrvačnosti vzhledem k ose otáčení. Během odrazu získá krasobruslař moment hybnosti, který zůstává stále stejný do dalšího odrazu78. Snížení momentu setrvačnosti musí tedy být doprovázeno zvýšením úhlové rychlosti. Krasobruslař tedy při upažení (zvýšení momentu setrvačnosti) snižuje úhlovou rychlost otáčení a naopak při připažení (snížení momentu setrvačnosti) úhlovou rychlost zvyšuje. Pro diváky je potom velmi atraktivní sledovat nekonečné variace změn rychlosti otáčení krasobruslařů v pestré nabídce akrobatických prvků.
Gymnasté, lyžaři, tanečníci, krasobruslaři a další sportovci kontrolují rychlost otáčení svého těla pomocí změny momentu setrvačnosti svého těla vzhledem k ose otáčení (sbalení-rozbalení, abdukce-addukce a další).
Interpretace druhého Newtonova zákona pro otáčivý pohyb těles
Změna momentu hybnosti tělesa je přímo úměrná výslednému momentu síly, který na toto těleso působí a tato změna má směr vnějšího momentu síly.
Pro dokonale tuhá tělesa, která mají stále stejný moment setrvačnosti kolem zvolené osy otáčení, můžeme popsat vztahy mezi kinematickými a kinetickými veličinami takto:
Jestliže na těleso působí výsledný vnější moment síly M (N·m), těleso získá úhlové zrychlení ε (rad/s2), které má směr tohoto momentu síly. Úhlové zrychlení bude přímo úměrné momentu vnější síly a nepřímo úměrné momentu setrvačnosti J (kg·m2) tělesa vzhledem k ose otáčení:
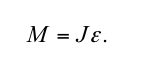
Pro tělesa, která nejsou dokonale tuhá, jako je například lidské tělo, výše uvedená rovnice neplatí. V případě lidského těla se výsledný vnější moment síly rovná rychlosti změny momentu hybnosti:

Výsledný moment vnější síly, který působí na těleso, je přímo úměrný rychlosti změny momentu hybnosti.
Změna momentu hybnosti se může projevit takto:
- snížení nebo zvýšení úhlové rychlosti
- změna polohy osy rotace
- změna momentu setrvačnosti
Úhlové zrychlení tělesa nebo změna momentu setrvačnosti nezbytně neznamená, že na těleso působí vnější moment síly, protože celkový moment hybnosti tělesa, které není dokonale tuhé, může zůstat nezměněn dokonce i tehdy, pokud těleso úhlově zrychluje nebo se mění jeho moment setrvačnosti.
Impuls momentu síly a moment hybnosti
Impuls momentu síly se rovná změně momentu hybnosti. Velikost změny momentu hybnosti závisí na době trvání působení momentu síly a jeho velikosti. Větší rameno síly vytváří větší moment síly, jak jsme již v předešlém textu uvedli. Zvýšení doby působení momentu síly se zdá být jednodušší ke zvýšení momentu hybnosti, ale při sportu hraje čas velice důležitou roli a není možné ho libovolně v určitých situacích prodlužovat. Ve výjimečných případech to však možné je. Krasobruslař například vytváří rotaci kolem longitudinální osy tak, že stojí na špičce nože jedné brusle a druhou se odráží od ledu. Noha, kterou se krasobruslař odráží, by měla být co nejdále od longitudinální osy, aby byl vytvořen co největší moment síly. Pokud krasobruslař své tělo uspořádá tak, že zaujme co nejmenší moment setrvačnosti vzhledem k longitudinální ose, potom při odrazu dostatečně zrychluje. Při dalším odrazu má již vysokou úhlovou rychlost a tím měně času na odraz. Proto může krasobruslař rozbalit své tělo, aby zvýšil moment setrvačnosti těsně před odrazem. Výsledkem většího momentu setrvačnosti je menší úhlová rychlost kolem longitudinální osy, tím více času na odraz, čím déle krasobruslař působí silou při odrazu tím větší impuls momentu síly byl udělen a tím dojde k větší změně momentu hybnosti.
Podobně diskaři na začátku hodu zaujmou polohu o maximálním momentu setrvačnosti a na konci vrhu při vypuštění disku je jejich moment setrvačnosti daleko menší. V aktivitách, u kterých je cílem rotovat co nejrychleji, sportovci zaujímají na začátku polohu o větším momentu setrvačnosti, aby mohli déle působit momentem síly a maximalizovat impuls momentu síly a tím změnu momentu hybnosti. Jakmile je vytvořen dostatečný moment hybnosti, sportovci zaujmou polohu o nižším momentu setrvačnosti a zvýší tak rychlost rotace ve správný okamžik, jako je například okamžik odhodu disku.
Interpretace třetího Newtonova zákona pro otáčivý pohyb těles
Moment síly, kterým působí první těleso na těleso druhé, vytváří stejně velký moment síly, jimž působí druhé těleso na první ve stejném čase, ale v opačném směru. Přitom nesmíme zapomenout na to, že tyto momenty síly mají stejnou osu rotace. Efekt těchto momentů sil je rozdílný, neboť působí na odlišná tělesa. Příkladem využití třetího Newtonova zákona pro otáčivý pohyb může být moment síly, který vytváří kvadriceps femoris (skupina vastus femoris) při extenzi v kolenním kloubu. Když dojde ke kontrakci těchto svalů, vzniká moment síly, který je příčinou rotace bérce v jednom směru a zároveň svaly vyvolávají stejně velký moment síly ale v opačném směru na stehno. Tyto dvě opačné rotace vytvářejí extenzi v kolenním kloubu.
Srovnání kinetických veličin posuvného a otáčivého pohybu
Tabulka 4 je užitečná při srovnání kinetických veličin posuvného a otáčivého pohybu. Můžeme zde pozorovat souhrn poznatků o kinetice posuvného a otáčivého pohybu, srovnat, v čem se navzájem kinetické veličiny otáčivého a posuvného pohybu liší a v čem jsou si naopak podobné.
| Posuvný pohyb | ||
| Veličina | Značka a definiční rovnice | Jednotka SI |
| Hmotnost (Mass) | m | kg |
| Síla (Force) | F | N |
| Hybnost (Momentum) | p = mv | kg·m/s |
| Impuls síly (Impulse) | I = ΣFΔt | N·s |
| Otáčivý pohyb pohyb | ||
| Moment setrvačnosti (Moment of inertia) | J = Σmr2 | kg·m2 |
| Moment síly (Torque nebo Momentum of force) | M = r x F | N·m |
| Moment hybnosti (Angular momentum) | L = Jω | kg·m2/s |
| Impuls momentu síly (Angular impulse) | H = ΣMΔt | N·m·s |
72 Poloměr gyrace je vzdálenost, která udává, jak daleko by musela být soustředěna veškerá hmotnost tělesa od osy rotace, aby vytvářela stejný odpor ke změně rotačního pohybu jako dané těleso v jeho původní podobě, tedy měla stejný moment setrvačnosti.Zpět
73 Předpokládáme stálou polohu osy otáčení vzhledem k tělesu.Zpět
74 Přesně by bylo možné vypočítat moment hybnosti lidského těla vzhledem k ose procházející těžištěm takto: L = Σ(Jiωi + mir2i/cgωi/cg), kde i označuje segment lidského těla a cg těžiště.Zpět
75 Při technicky správně provedeném běhu na delší vzdálenost by nemělo docházet k rotaci a náklonům trupu.Zpět
76 Výjimkou jsou případy, kdy se lidské tělo začne otáčet vlivem odporu prostředí (vody, vzduchu). Příčinou tzv. druhotné rotace, nastávající až po odraze, je Coriolisova síla, která je vyvolána pohybem segmentu lidského těla mimo aktuální rovinu rotace těla. Zpět
77 Moment hybnosti zůstává stejný, pokud nepůsobí žádný výsledný vnější moment síly, který vzniká při kontaktu člověka s jiným tělesem.Zpět
78 Při zanedbání tření.Zpět