Force
Static Equilibrium

Statics is the branch of mechanics studying forces that act on bodies in static or dynamic equilibrium. Static equilibrium is a state where bodies are at rest; dynamic equilibrium is a state where bodies are moving at a constant velocity (rectilinear motion). In both cases the sum of the forces acting on them is zero.
Free Body Diagram
Free body diagram pictures a body of interest (athlete) and external forces acting on it.
Figure 5 Free body diagram14. FR is the sum of reaction forces acting on both legs15 and FG is gravitational force acting on athlete’s body.

Let us imagine a simple situation of an athlete standing on the ground (Fig. 5). There are two forces acting on the athlete. The first one is non-contact gravitational force. If only this force were acting on the athlete, he/she would by moving downwards with the acceleration of 9,81 ms-2. As this is obviously not the case, there must exist another force causing the state of static equilibrium, so that the athlete is at rest. This is the reaction force of the ground acting upward on the athlete’s feet.
Free body diagram is a valuable tool allowing to carry out mechanic analysis.
Static Analysis
Mathematically the situation of a standing person can be described as follows:
ΣF = o
This is the equation of static equilibrium. The expression ΣF represents the resultant external force, in other words a vector sum of forces acting on a standing person; o is zero vector (0, 0, 0).
If forces acting on a person lie in one line, we can simply add them up. Their upward direction is marked as positive, their downward direction as negative.
In the case of a standing person the reaction force of the ground acts upward on the human body and, in line with our convention, has positive direction. However, its magnitude is unknown to us. Gravitational force acts downward and therefore has negative direction.
If only two forces act on a body in the state of either static or dynamic equilibrium, they have equal magnitude but opposite direction.
Weightlifter with the weight of 70 kg has lifted a barbell with the weight of 90 kg and is holding it above his head (Fig. 6). As long as he is holding the barbell, both bodies (weightlifter and barbell) are in static equilibrium. What is the force that must act on the weightlifter’s feet to keep him in static equilibrium?
Figure 6 Free body diagram – weightlifter with a barbell.
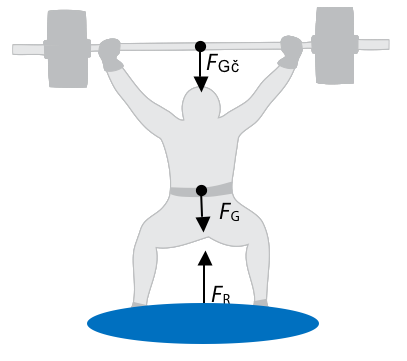
If we consider the case of both bodies (weightlifter and barbell) together, the solution may be quite simple. We sum up the weights of both bodies. The resultant reaction force acting on the weightlifter’s feet is then the total of these two gravitational forces, but with opposite (i.e. upward) direction. The force FR equals 1570 N, i.e. the weight of the weightlifter plus the weight of the barbell, and acts vertically upward.
In the case that the forces acting on a body are not in one line and their directions are neither vertical, nor horizontal, we have to resolve these forces into their horizontal and vertical components. Then we solve static equilibrium equations, separately for vertical and horizontal directions. After that we will calculate the magnitude of the resultant force with the use of the Pythagoras’ theorem and its direction with the use of trigonometry.
14 The centre of gravity is shifted up against the 3rd and 4th sacral vertebrae. The athlete is not standing in basic anatomical posture.Zpět
15 In reality reaction forces originate in the place of contact between the feet and the ground. However, for the sake of this free body diagram we can plot the resultant reaction force whose point of application is in so called „centre of pressure”, i.e. away from the place of contact between the feet and the ground.Zpět