
Cílem studie bylo analyzovat nejdůležitější parametry určující pohybovou strukturu základního skoku klasického tance – grand jeté. Výzkumný soubor tvořilo 8 studentů Taneční konzervatoře v Brně. S využitím systému Simi Motion jsme provedli 3D kinematickou analýzu zkoumaného skoku. Na základě srovnání kvality provedení a naměřených dat skoku grand jeté jsme určili optimální hodnoty podstatných parametrů limitujících kvalitu provedení. Rychlost vzletu by měla dosahovat hodnoty přibližně 2,4 m∙s-1, optimální úhel vzletu je 28–30 °. Odrazová dolní končetina by měla švihnout do zanožení ihned na začátku letové fáze s minimální rychlostí 3,3 m∙s-1. Dosahují-li pohybové schopnosti tanečníků nadprůměrné úrovně potřebné pro optimální provedení skoků klasického tance, umožňují jim určitou variabilitu struktury daného prvku.
Klasický tanec je pohybové umění, které je jak fyzicky, tak psychicky velmi náročné. Podstatou klasického tance je řešení daného pohybového úkolu přesně, dokonale a zároveň esteticky. K optimální realizaci je zapotřebí vytrvalostních, silových, rychlostních i koordinačních schopností. Vysoká flexibilita je také nezbytnou podmínkou pro provedení mnoha prvků. Taneční pohybová skladba vyžaduje velký počet osvojených pohybových dovedností, jejichž struktura je často velmi složitá. Snahou je popsat fyzikální principy, které vytvoří základnu pro pochopení časoprostorové i dynamické struktury konkrétních tanečních pohybů. Samotné pochopení mechanizmu pohybu neumožní tanečníkovi provést pohyb, který přesahuje jeho pohybové schopnosti, avšak ukáže mu cestu, která vede k úspěšné realizaci pohybu. Tato znalost také umožňuje přesně rozlišit, které aspekty pohybu jsou záležitostí stylu a které přímo ovlivňují pohyb v jeho podstatě. Věda má tedy i v klasickém tanci své důležité, nenahraditelné místo. Z toho důvodu se v práci zaměřujeme na analýzu struktury základního baletního skoku grand jeté z hlediska biomechaniky. Grand jeté patří mezi vzdušné vysoké skoky z místa s odrazem z jedné nohy a doskokem na druhou. Grand jeté se učí jako jeden z prvních vysokých skoků, v osnovách osmileté taneční konzervatoře je zařazen do pátého ročníku. Přesné provedení popisuje Tarasov (1983), Bazarovová (1985), Vaganová (1981) a Kostrovickaja a Pisarev (1986).
Cíl studie
Cílem studie bylo analyzovat nejdůležitější parametry určující pohybovou strukturu základního skoku klasického tance grand jeté.
Metody
Výzkumný soubor
Zkoumaný soubor tvoří studentky Taneční konzervatoře Brno. Jde o skupinu, která byla vytvořena záměrným výběrem. Testováno bylo 8 tanečnic z 6. a 7. ročníku. Tento poměrně nízký počet probandů odůvodňujeme omezeným počtem dostupných studentek tanečních konzervatoří a náročností sběru a zpracování dat. Průměrná výška zkoumaného souboru byla 167,4 cm, průměrná hmotnost 56,6 kg, věk tanečnic se pohyboval v rozmezí 16–18 let a doba, po kterou byly tanečnice odborně tanečně vzdělávány, dosahovala 6 až 7 let. Výzkumný soubor studentek taneční konzervatoře považujeme za homogenní vzhledem k předpokladu určité úrovně pohybových schopností při splnění kritérií talentových zkoušek pro přijetí na tento studijní obor.
Metody měření a vyhodnocování dat
Pomocí systému Simi Motion jsme provedli 3D kinematickou analýzu skoku grand jeté. Každá testovaná osoba (TO) skočila třikrát s odrazem z pravé dolní končetiny a třikrát z levé dolní končetiny. Vzhledem k tomu, že počet testovaných osob byl 8, analyzovali jsme celkem 48 skoků grand jeté.
Pro snímání obrazu jsme použili dvě vysokofrekvenční synchronizované digitální kamery Simi Motion Version 7. Zaznamenaná data jsme zpracovávali v programu taktéž Simi Motion.
Jednotlivá naměřená data jsme individuálně posoudili. Následně jsme tato data srovnali s výsledky odborného posouzení jednotlivých skoků, které provedla doc. Vondrová, odbornice na klasický tanec, pedagožka Taneční konzervatoře i Janáčkovy akademie múzických umění v Brně. Model optimálního provedení skoku jsme vytvořili na základě vypracované 3D kinematické analýzy konkrétních skoků, které byly doc. Vondrovou ohodnoceny nejlépe.
Video 1 Skok grand jeté z pravé končetiny - pohled 1
Video 2 Skok grand jeté z pravé končetiny - pohled 2
Video 3 Skok grand jeté z pravé končetiny - pohled 3
Video 4 Skok grand jeté z levé končetiny - pohled 1
Video 5 Skok grand jeté z levé končetiny - pohled 2
Video 6 Skok grand jeté z levé končetiny - pohled 3
Výsledky
U všech tanečních skoků, včetně grand jeté, rozlišujeme čtyři fáze:
- příprava
- odraz
- let
- doskok
1. fáze – příprava
Příprava plní funkci rozběhu. Tanečník získává ještě před odrazem určitou dopřednou rychlost, která po efektivním využití zkvalitní provedení skoku, zejména odrazovou fázi.
2. fáze – odraz
Základním předpokladem pro odraz je přiměřená pevnost podložky, vzhledem k níž dojde k přemístění těžiště těla. V přípravné fázi odrazu dochází ke zmenšování úhlů mezi články odrazové končetiny. Současně s touto flexí dochází k protažení odrazových svalů. Proti tomuto protažení působí pružná síla, a to vede ke zvýšení potenciální elastické energie svalů. Ta se následně přemění v energii kinetickou. Pro převedení vodorovné rychlosti získané rozběhem do šikmého směru je nutné částečně „vzpříčit“ odrazovou končetinu při jejím dokroku, přičemž jsou její svaly setrvačností stlačovány. Vlastní odraz je způsoben akční silou odrazových svalů a reakční silou podložky. Tato práce je podpořena švihem volné dolní končetiny, případně i horních končetin, a následným přenosem hybnosti na trup. Thomas et al. (2004) provedli dynamickou analýzu skoku grand jeté a měřili reakční síly podložky, momenty těchto sil během fáze odrazu i síly během fáze doskoku. Vodorovná rychlost částečně převedená do šikmého směru se částečně projeví jako setrvačná síla ve směru vodorovném. Grand jeté vyžaduje šikmý odraz. Podle Kašparové (1981) je mechanickým principem odrazu to, že jsou do něho nejdříve zapojovány nejvzdálenější segmenty od opory a odraz dokončují ty nejbližší, tedy kloub hlezenní a klouby metatarzální. Dále uvádí jako podmínku pro efektní odraz, aby pata byla v kontaktu s podložkou. Tak bude lýtkový sval smršťován až při samotném odrazu a nikoli dříve. Odrazová síla, jejímž účinkem je translační pohyb těla, prochází místem opory a směřuje do těžiště, které je před oporou. Toto předsunutí těžiště, tedy úhel mezi podložkou a odrazovou silou, má přímý vliv na velikost elevačního úhlu.
Graf 1 Rychlost kotníku švihové dolní končetiny. V grafu je vyznačena rychlost v okamžiku, kdy odrazová dolní končetina opouští podložku.
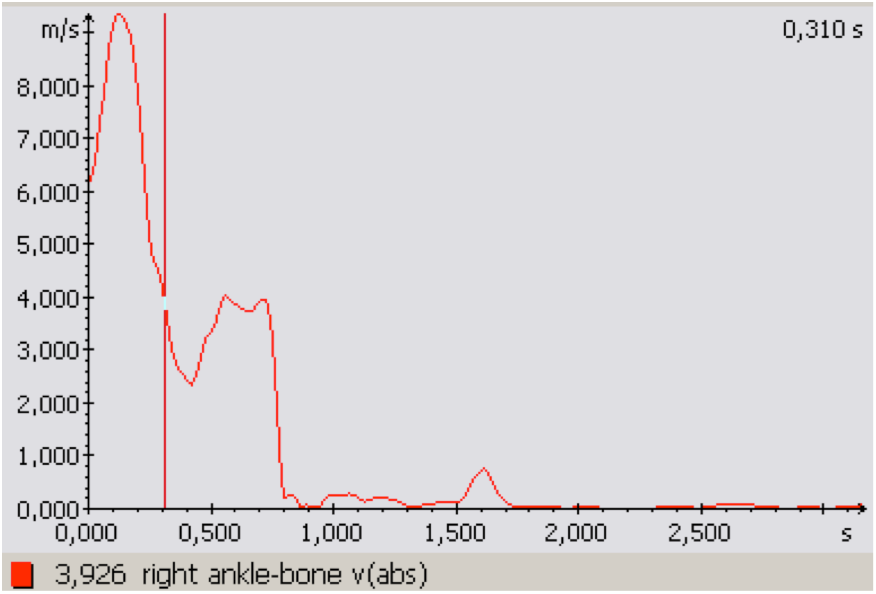
V přípravné fázi doskakovala nejlepší tanečnice na odrazovou DK z přípravného poskoku rychlostí 2,694 m∙s-1. Přechod z maximální flexe v kyčelním, kolenním a hlezenním kloubu odrazové DK do extenze dokončené ve chvíli opuštění podložky trval 0,19 s. Tanečnice dosáhla vzletové rychlosti 2,574 m∙s-1. Úhel vzletu těžiště byl 43 °, tedy o 13 ° vzdálen od hranice optimálního úhlu (28–30 °). Tanečnice by tedy měla optimálně vzlétnout pod menším úhlem, což by jí napomohlo vytvořit plošší a delší skok. Vzletovou rychlost ovlivnil i pohyb horních končetin, především však švih pravé DK. Maximální rychlost, které kotník švihové DK dosáhl, byla 9,352 m∙s-1, a to ve chvíli míjení odrazové DK. Ve chvíli vzletu byla rychlost kotníku švihové DK 3,926 m∙s-1 (graf 1).
3. fáze – let
Po odrazu dochází k přerušení opory těla o podložku. Součtem vodorovné rychlosti a šikmé rychlosti způsobené odrazem se těžiště těla začne pohybovat vzhůru pod elevačním úhlem α s počáteční rychlostí v0. Leško a kol. (2006) dokazují, že je to právě impuls síly, co ovlivňuje velikost v0, a v důsledku toho i výšku výskoku. Vodorovné a svislé složky veličin popisujících pohyb těžiště jsou na sobě nezávislé. Na poměru jejich velikostí však závisí úhel vzletu. Zanedbáme-li působení odporu vzduchu, vodorovná složka rychlosti pohybu má konstantní hodnotu v0x. Velikost svislé složky rychlosti je proměnná. V okamžiku, kdy je tato složka rychlosti rovna nule, dosahuje tělo nejvyššího bodu své trajektorie. V tomto kulminačním bodě skoku jsou dolní končetiny roznoženy na 150 ° (Tarasov, 1983). Trajektorie, po které se těžiště pohybuje, je určena velikostí a směrem rychlosti v závěru odrazu a v letu ji již nelze měnit. Laws (2002) ve své publikaci zdůrazňuje vytvoření iluze letu, která může být vytvořena změnou tělesné konfigurace během letu. Ačkoli těžiště sleduje parabolickou křivku, může být změněna relativní poloha těžiště vůči tělu. Ve chvíli, kdy tanečník opouští podložku, jsou jeho horní i dolní končetiny spíš níže a těžiště těla se nachází v abdominální oblasti. Když dále těžiště stoupá po parabolické křivce, zvedáním horních i dolních končetin se těžiště v těle zvedne výš. Při optimálním načasování vznikne iluze horizontálního letu. Zákon zachování momentu hybnosti tento jev objasňuje. Robertson et al. (2004) se zabýval podmínkami vytvoření iluze letu. Probandi, které testoval, však nebyli schopni tuto iluzi vytvořit.
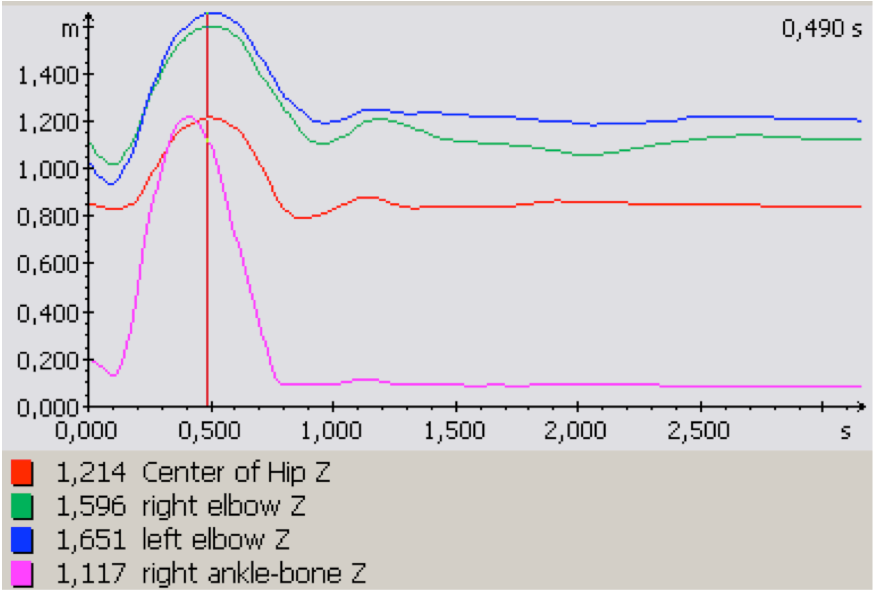
V letové fázi jsme se zaměřili především na časovou koordinaci pohybu dolních i horních končetin vzhledem k poloze těžiště v daném okamžiku. Srovnávali jsme časovou posloupnost, ve které dosáhly maximální výšky hlava, těžiště, švihová DK a horní končetiny (graf 2). Švihová DK dospěla do maximální výšky o 0,08 s dříve než těžiště a o 0,11 s dříve než hlava. Odrazová DK po odrazu přešla do zanožení, přičemž její kotník dosáhl maximální rychlosti 3,422 m∙s-1. Pohyb horních končetin bohužel netrval déle než stoupání těžiště těla, čímž se tanečnice omezila ve vytváření „iluze horizontálního letu“.
Graf 2 Graf ukazuje načasování maximální výšky švihové DK a HK vzhledem k pohybu těžiště. V grafu je vyznačen okamžik, kdy se těžiště nachází v nejvyšším dosaženém bodě.
Graf 3 Ukazuje načasování pohybu dolních končetin vzhledem k pohybu těžiště a hlavy. V grafu je vyznačen okamžik, kdy se těžiště nachází v nejvyšším dosaženém bodě.
Obr. 5 Grand jeté – mikrofáze letu ve chvíli, kdy jsou kotníky ve stejné výšce
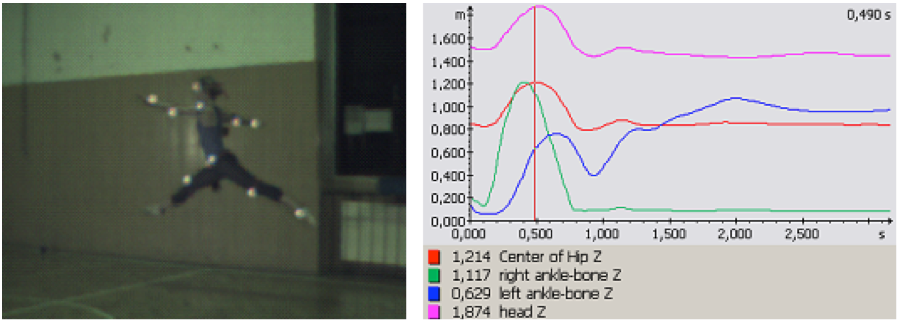
Dále jsme v letové fázi srovnávali dobu, ve které těžiště dosáhlo maximální výšky, s dobou, kdy se kotník pravé i levé DK nacházely ve stejné výšce (obr. 5). Okamžik, kdy byly oba kotníky ve stejné výšce, byl oproti těžišti opožděn o 0,09 s (graf 3). Je však důležité soustředit pozornost také na to, v jaké fázi pohybu dolních končetin tento okamžik nastává. Optimální je, když se v této chvíli zanožená DK nachází ve své maximální výšce. To se tanečnici podařilo, neboť se kotník této DK následně zvedl pouze o zanedbatelných 1,6 cm. Velikost úhlu roznožení mezi dolními končetinami se v tomto okamžiku dostala na 109,32 °, což není optimální rozsah.
4. fáze – doskok
Poslední fází grand jeté je doskok, při němž se tělo dostává opět do kontaktu s podložkou oporou jednonož. Při doskoku je tělo setrvačností stlačováno dolů, což je třeba regulovat amortizační prací svalů. Aby svaly mohly takto pracovat co nejúčinněji a nejdéle, je třeba, aby před doskokem byla končetina úplně propnuta a aby její svaly byly v izometrickém napětí (Kašparová, 1981). Vodorovná složka setrvačných sil působících na těžiště přesouvá těžnici k okrajům plochy opory, která je na začátku doskoku poměrně malá, nebo až za ni. V tomto případě již tělo začíná přepadávat působením otáčivých účinků tíhové síly. Aby tanečník v tomto případě zabránil přepadávání, musí doskakovat na mírně přednoženou dolní končetinu tak, aby setrvačné síly procházely těžištěm a nevznikal moment otáčení. Podle Tarasova (1983) má být doskoková končetina v přednožení na 45 °, zatímco druhá zůstává v zanožení pod úhlem 90 ° od vertikály. Kašparová (1981) ve svém výzkumu došla k závěru, že při doskoku začíná první zmenšování úhlů v kloubech metatarzálních, následně kolenních a kyčelních se současným zabrzděním změny úhlů v kloubech hlezenních. Přidržení paty nad zemí je nutné k tomu, aby nedošlo k prudkému nárazu celého chodidla. Setrvačné síly působící na trup a horní končetiny vedou k předklonu trupu, a tak mohou narušit dynamickou rovnováhu. Proto je nutná izometrická kontrakce zádových svalů, která tyto segmenty těla imobilizuje.
Ve fázi doskoku jsme se soustředili především na úhel dopadu a jemu příslušné přednožení doskokové DK. Z kinogramu (obr. 5) je patrné, že DK, na kterou tanečnice doskočila, se pohybovala po téměř stejné trajektorii, po které následně klesalo těžiště. Ve chvíli doskoku tedy setrvačná síla procházející těžištěm směřovala téměř do místa kontaktu chodidla s podložkou. Délka skoku měřená z místa, odkud se tanečnice odrazila, do místa, kam doskočila, byla 1,27 m. Doba letové fáze byla 0,44 s.
Graf 4 Ukazuje rozsah vertikálního pohybu kotníku zanožené dolní končetiny a ramen po doskoku po došlápnutí na celé chodidlo stojné dolní končetiny.
Obr. 6 Kinogram skoku grand jeté
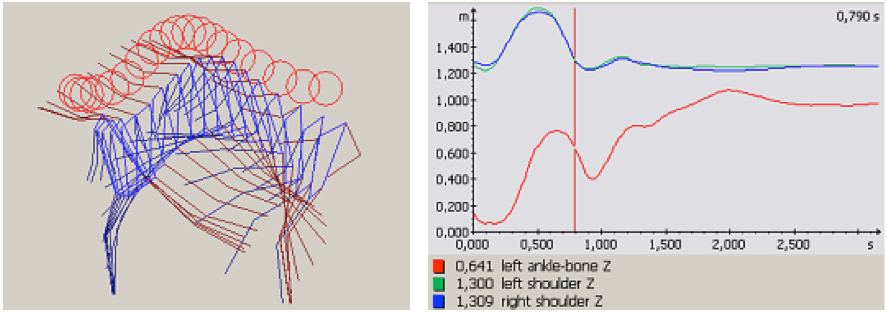
Dále jsme zjišťovali rozsah pohybu trupu a zanožené DK ve fázi doskoku (obr. 6). U této tanečnice jsme zaznamenali větší pokles zanožené dolní končetiny (24 cm) od chvíle došlápnutí na celé chodidlo, což nemůžeme považovat za optimální provedení. Tento pohyb je třeba ještě více minimalizovat. Kotník dolní končetiny, na kterou tanečnice doskočila, ještě urazil dráhu 0,228 m, než se ustálil. Snahou je tento pohyb také co nejvíce omezit. Ve srovnání s jinými naměřenými hodnotami u ostatních tanečnic tuto hodnotu považujeme ještě za přijatelnou.
Diskuze
Množství získaných dat z analýz 48 skoků grand jeté umožňuje vyhodnotit nejčastější chyby, kterých se tanečnice při provedení tohoto skoku dopustily.
Ve fázi odrazu to bylo především nevyužití celého potenciálu odrazové DK, zejména svalu lýtkového, když se tanečnice neodrážely z celého chodidla. Z přípravného poskoku došláply jen na pološpičku, čímž zmenšily odraz, následně tak i velikost vzletové rychlosti a dobu letové fáze. Dalším nedostatkem je pomalý švih DK do přednožení, čímž se snižuje hybnost této DK a na trup se tak v následujícím okamžiku přenáší této hybnosti méně. Některé tanečnice provedly švih dostatečně rychle, avšak časově ho nezkoordinovaly s odrazem druhé DK. Ve většině případů proběhl odraz o něco později, než by bylo optimální. Také odrazová DK prováděla často odraz pod větším než optimálním úhlem. V důsledku tohoto odchýleného směru odrazové síly a v důsledku uvedeného opožděného dokončení odrazu DK vzlétly (až na jednu výjimku) všechny tanečnice pod větším úhlem než je optimálních 28–30 °, tedy příliš kolmo vzhůru. Některým tanečnicím se při švihu paží nepodařilo zachovat svůj ladný a estetický pohyb vedený podle pravidel klasického tance.
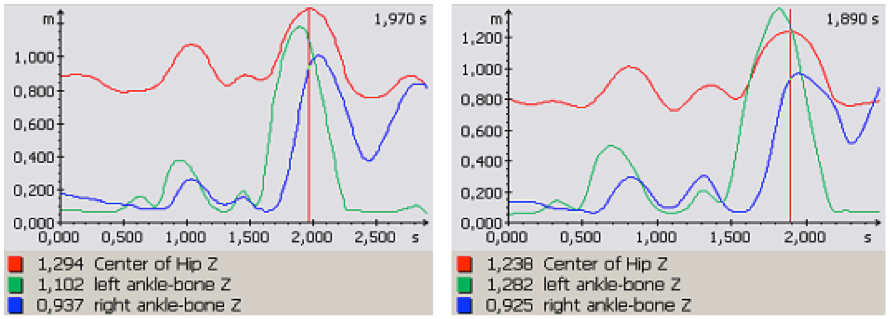
V letové fázi je nejpodstatnější rychlý švih odrazové DK do zanožení. V tomto jsme také zaznamenali nejvíce nedostatků, které se výrazně projeví na vzájemné poloze všech segmentů těla v průběhu letové fáze. Provede-li tanečnice pomalý švih do zanožení, přednožená DK mezitím příliš klesne. Potom dojde k tomu, že přednožená DK je již téměř dole, zatímco druhá DK se do zanožení teprve zvedá. Vidíme tak jakési překlopení dolních končetin místo současného rozšvihnutí. Místo, ve kterém se pak kotníky míjí, je velmi nízko. Rozdíl je velmi dobře vidět na grafech (graf 5 a, b). Na grafu a) baletka optimálně načasovala moment, ve kterém jsou oba kotníky ve stejné výšce. Tento okamžik nastal téměř ve stejnou dobu, kdy těžiště dosáhlo svého maxima, švihová DK byla v počáteční fázi klesání a odrazová těsně před dosažením své maximální výšky. Na grafu b) vidíme, že rychlost zašvihnutí nebyla dostačující, a tak zanožená DK nedosáhla potřebné výšky. Je znát podstatný rozdíl mezi maximem, kterého dosáhla odrazová a švihová DK. Kvalitu letové fáze často limitovalo malé roznožení dolních končetin. V odrazové i letové fázi je u některých tanečnic znatelné špatné natočení ramen nebo pánve. Osa ramen i pánve by měla během skoku zůstat kolmá ke směru pohybu.
Graf 5 a) optimální načasování pohybu dolních končetin, b) chybné načasování pohybu dolních končetin u skoku grand jeté. V grafech je vyznačen okamžik, kdy se těžiště nachází v nejvyšším dosaženém bodě.
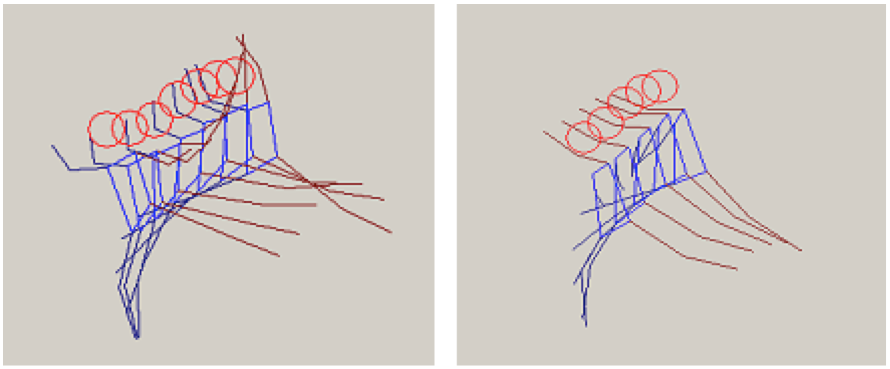
V závěrečné fázi skoku grand jeté je nejdůležitější co nejdříve nabýt rovnováhy a udržet ji. Některé tanečnice doskakovaly na příliš sklopenou DK. Setrvačná síla pak neprochází místem kontaktu chodidla s podložkou, ale před ním. Vzniká tak moment otáčení a tanečnice přepadává dopředu. V důsledku toho poskakuje vpřed, aby se dostala do rovnovážné polohy. Srovnání ukazují obrázky 7a, b. Na obr. 7a vidíme příliš sklopenou DK, na kterou tanečnice doskakuje, na obr. 7b je již přednožení optimální. Další častý nedostatek jsme pozorovali u zanožené DK, která často při doskoku vlivem setrvačnosti příliš klesla, taktéž trup se setrvačností příliš předklonil. Tento negativní jev je způsobený nedostatečným napětím svalů udržujících DK v zanožení a vzpřimovačů trupu.
Obr. 7 a) chybný doskok, b) optimální doskok
Shrnutí
Provedenou 3D kinematickou analýzou jsme zjistili kinematické parametry charakterizující časoprostorovou strukturu základního skoku klasického tance grand jeté. Skoky a jejich konkrétní fáze, které byly odbornicí ohodnoceny jako špatně provedené, se i v naší 3D kinematické analýze jevily jako podprůměrné. Na základě porovnávání kvality struktury a naměřených hodnot příslušných parametrů skoků se nám podařilo stanovit základní požadavky na provedení grand jeté. Cílem tanečníků má být co nejdelší dráha letu, vytvoření iluze „letu“ v blízkosti vrcholu parabolické křivky, po níž se těžiště pohybuje, a stabilní doskok bez nadbytečných pohybů. Z 3D kinematické analýzy vyplývá, že přímý vliv na splnění uvedených požadavků mají tyto parametry: získaná vzletová rychlost a úhel vzletu ve fázi odrazu, vzájemná koordinace pohybu dolních a horních končetin a jejich načasování vzhledem k pohybu těžiště ve fázi letu a rozsah pohybu trupu a zanožené dolní končetiny ve fázi doskoku. Na základě výsledků 3D kinematické analýzy konkretizujeme optimální hodnoty těchto základních parametrů. Dospěli jsme k závěru, že rychlost kotníku švihové DK by měla ve svém maximu dosáhnout hodnoty 8,5 m∙s-1. Tento rychlý švih musí být podpořen i rychlou extenzí odrazové DK. Vzletová rychlost těžiště by měla dosahovat hodnoty minimálně 2,4 m∙s-1. Co se týče úhlu vzletu, je podle nás možné provést kvalitní skok tehdy, je-li odchylka od optimálního úhlu vzletu (28–30 °) do 8 °. V počátku letové fáze provádí odrazová DK švih do zanožení. Kotník by měl dosáhnout maximální rychlosti o velikosti nejméně 3,3 m∙s-1. Jsou-li všechny tyto fáze provedeny v přijatelné kvalitě, i fáze doskoku bude s největší pravděpodobností optimální, protože při udržování dynamické rovnováhy nemusí kotník korigovat tolik rušivých pohybů. Jako optimální můžeme přijmout doskok, při kterém neurazí kotník dráhu větší než 0,22 m.
Všechny získané výsledky ukazují na skutečnost, že realizace skoků má více individuálních biomechanických řešení. Ta závisí především na kondičních a koordinačních dispozicích tanečnic a na dalších faktorech. Dosahují-li tyto pohybové schopnosti vysoké úrovně nezbytné pro kvalitně provedený skok, je v rámci optimálního řešení daného pohybového úkolu možná jistá variabilita struktury tanečního skoku.
(brož. vaz., s. 21 - 37)